Page 115 - chapter 1

115
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

ΠΑΡΑΔΕΙΓΜΑΤΑ

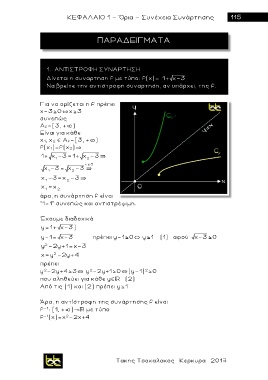
1. AΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ
Δίνεται η συναρτηση f με τύπο: f(x)= 1 x 3
Να βρείτε την αντιστροφη συναρτηση, αν υπάρχει, της f.

Για να ορίζεται η f πρέπει
χ-3 0`χ 3
συνεπώς
Α f=[3, + )
Είναι για κάθε
x 1, x 2 Α f=[3, + )
f(x 1)=f(x 2)~
1+ x -3= 1+ x -3~
1 2
x 3
x -3 = x -3 ~
1
2
x -3=x -3~
1 2
x =x
2
1
άρα, η συνάρτηση f είναι
"1-1" συνεπώς και αντιστρέψιμη.

Έχουμε διαδοχικά
y= 1+ x-3 )

y-1= x-3 πρέπει y-1 0` y 1 (1) αφού x-3 0
y -2y+1=x-3
2
2
x=y -2y+4
πρέπει
y -2y+4 3` y -2y+1 0`(y-1) 2 0
2
2
που αληθεύει για κάθε y (2)
Από τις (1) και (2) πρέπει y 1

Άρα, η αντίστροφη της συνάρτησης f είναι
f - 1 : [1, + ) με τύπο
f - 1 (χ)=χ -2χ+4
2

Τακης Τσακαλακος Κερκυρα 2017