Page 111 - chapter 1

111
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

άρα f(ρ)=ρ, δηλαδή ρ είναι ρίζα της f(x)=x και αφού ρ ρίζα
της f(x)=f - 1 (x), τότε οι δύο εξισώσεις είναι ισοδύναμες.

Α ν τ ί σ τ ρ ο φ α

● Aν ρ Α (και ρ f(Α)) είναι μία ρίζα της f(x)=x τότε
f(ρ)=ρ (1)
και
f 1 f 1 (f(ρ))
f(ρ)= ρ ~ f (f(ρ))= f (ρ) ~ ρ= f (ρ 1 )~ f(ρ)= f (ρ)
-1
1
1
αφου f για καθε ρ f(A)
δηλαδή ρ είναι ρίζα f(x)=f - 1 (x) και αφού ρ ρίζα της f(x)=x,
τότε οι δύο εξισώσεις είναι ισοδύναμες.
ΣΥΜΠΕΡΑΣΜΑ
Τα συστήματα
y= f(x) y= f(x) y= x
(Σ )= , (Σ )= και (Σ )=
1 2 3 1
y= f (x) y= x y= f (x)
1
είναι ισοδύναμα.

3.
Έστω η αντιστρέψιμη συνάρτηση f:A και η f - 1 :f(A)
Tα γραφήματα τους είναι συμμετρικά ως προς την ευθεία

y=x, που δεν είναι απάραιτητα μοναδική.

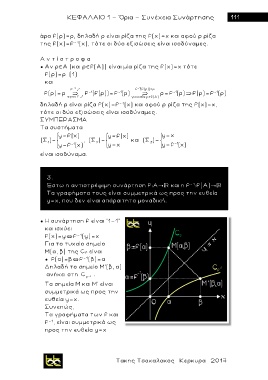
● Η συνάρτηση f είναι "1-1"
και ισχύει
f(x)=y`f - 1 (y)=x
Για το τυχα ί ο σημείο

Μ(α, β) της C f είναι
● f(α)=β`f - 1 (β)=α
Δηλαδή το σημείο Μ'(β, α)
α ν ήκει στη C 1 .
f
Tα σημεία Μ και Μ' είναι
συμμετρικά ως προς την
ευθεία y=x.
Συνεπώς,
Tα γραφήματα των f και
f - 1 , είναι συμμετρικά ως
προς την ευθεία y=x

Τακης Τσακαλακος Κερκυρα 2017