Page 112 - chapter 1

112
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

● Μη μοναδικότητα ...
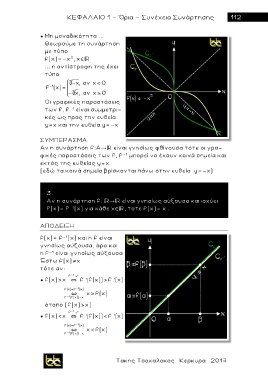
Θεωρούμε τη συνάρτηση
με τύπο
3
f(x)=-x , x
... η αντίστροφη της έχει
τύπο
3 -χ , αν χ< 0
-1
f (x)=
- χ , αν χ 0
3
Οι γραφικές παρ α σ τ άσεις
των f, f - 1 είναι συμμετρι-

κές ως προς την ευθεία
y=x και την ευθεία y=-x

ΣΥΜΠΕΡΑΣΜΑ
Αν η συνάρτηση f:A είναι γνησίως φθίνουσα τότε οι γρα-
φικές παρ α σ τ άσεις των f, f - 1 μπορεί να έχουν κοινά σημεία και
εκτός της ευθείας y=x
(εδώ τα κοινά σημεία βρίσκονται πάνω στην ευθεία y=-x)

3.
Αν η συνάρτηση f: είναι γνησίως αύξουσα και ισχύει
f(x)= f - 1 (x) για κάθε χ , τοτε f(x)= χ .

ΑΠΟΔΕΙΞΗ

f(x)= f - 1 (x) και η f είναι
γνησίως αύξουσα, άρα και
η f - 1 είναι γνησίως αύξουσα
Έστω f(x) χ
τότε αν:

f - 1
● f(x)>χ f -1 (f(x))> f (x)
-1
f(x) = f -1 (x)
x> f(x)
f -1 (f(x)) = x
άτοπο (f(x)>χ)

f - 1
● f(x)<χ f -1 (f(x))< f (x)
-1
f(x) = f -1 (x)
x< f(x)
f -1 (f(x)) = x

Τακης Τσακαλακος Κερκυρα 2017