Page 118 - chapter 1

118
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

4. AΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ
Δίνεται η συνάρτηση f: για την οποία ισχύει
f (x)+ f(x)-e =0 για κάθε χ
3
x
α) Να αποδείξετε ότι η συνάρτηση f είναι αντιστρέψιμη.
β) Να βρείτε την αντίστροφη συνάρτηση, αν υπάρχει, της
f.

α )
Το πεδίο ορισμού της f είναι:Α=
Για κάθε χ η δοσμένη σχέση: f (x)+ f(x)=e (1)
3
x

είναι δ ι αδοχικά

f(x )= f(x )
f(x )= f(x )` 1 2
1 2
f (x )= f (x )
3
3
1 2
( )
` f (x )+f(x )= f (x )+f(x )
3
3
1 1 2 2
(1 )
`e x 1 = e x 2
`x = x 2
1
άρα, η συνάρτηση f είναι "1-1",
οπότε αντιστρέφεται

β )
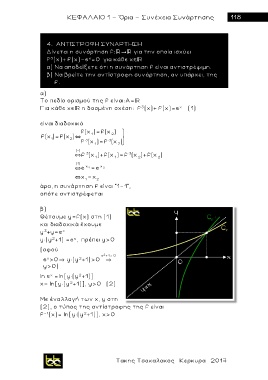
Θέτουμε y=f(x) στη (1)
και διαδοχικά έχουμε
y +y=e
x
3
y (y +1) =e , πρέπει y>0
x
2
(αφού
2
χ + 1 > 0
e >0~ y (y +1)>0 ~
x
2
y>0)
ln e =ln[y (y +1)]
x
2
x= ln[y (y +1)], y>0 (2)
2

Με έναλλαγή των x, y στη
(2), ο τύπος της αντίστροφης της f είναι
2
f - 1 (x)= ln[y (y +1)], χ>0

Τακης Τσακαλακος Κερκυρα 2017