Page 63 - chapter 1

63
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

Θ Ε Ω Ρ Ι Α ...

ΟΡΙΣΜΟΣ
Δύο συναρτήσεις f και g θα λέγονται ί σ ε ς αν και μόνο αν
έχουν:
● To ί δ ι ο πεδίο ορισμού Α και
● Για κ ά θ ε x A ισχύει f(x) = g(x)

ΠΑΡΑΤΗΡΗΣΕΙΣ

● Για να δηλώσουμε οτι δύο συναρτήσεις f και g είναι ίσες

γ ρ άφουμε f = g.

● Αν δύο συναρτήσεις f και g έχουν διαφορετικά πεδία ορισμού
Α f, Α g και υπάρχει ένα κοινό υποσύνολο τους Ε, για το οποίο

ισχύει f(x)=g(x) για κάθε x Ε, τότε θα λέμε οτι οι συναρτή-

σεις f και g είναι ίσες στο σύνολο Ε .

● Αν για τις συναρτήσεις f και g δεν ισχύει μία τουλάχιστον
α π o τις προυποθέσεις του ορισμού, αυτές είναι διάφορες

μεταξύ τους και γ ρ άφουμε f g.

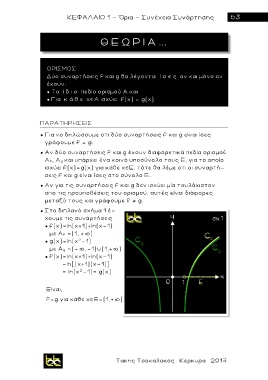
● Στο διπλανό σχήμα 1 έ-
χουμε τις συναρτήσεις

● f(x)=ln(x+1)+ln(x-1)

με Α f =(1, + )
● g(x)=ln(x -1)
2

με Α g =(- ,-1) (1,+ )

● f(x)=ln(x+1)+ln(x-1)
=ln[(x+1)(x-1)]

= ln(x -1)= g(x)
2

Eίναι,

f=g για κάθε χ Ε=(1,+ )

Τακης Τσακαλακος Κερκυρα 2017