Page 68 - chapter 1

68
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

ΠΑΡΑΔΕΙΓΜΑΤΑ

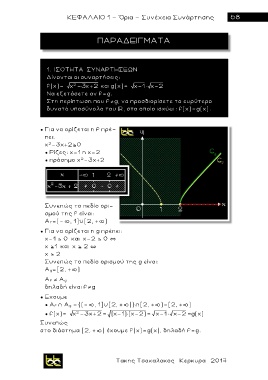
1. ΙΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ
Δίνονται οι συναρτήσεις:
f(x)= x 2 3 x 2 και g(x)= x 1 x 2
Nα εξετάσετε αν f=g.
Στη περίπτωση που f g, να προσδιορίσετε το ευρύτερο
δυνατό υποσύνολο του , στο οποίο ισχύει : f(x)=g(x).

● Για να ορίζεται η f πρέ-
πει:
χ -3χ+2 0
2
● Ρίζες: χ=1 η χ=2
● π ρ όσημο χ -3χ+2
2

Συνεπώς το πεδίο ορι-
σμού της f είναι:
Α f=(- , 1] [2, + )

● Για να ορίζεται η g πρέπει:
χ-1 0 και χ-2 0 `
χ 1 και χ 2 `
χ 2

Συνεπώς το πεδίο ορισμού της g είναι:
Α g=[2, + )

Α f Α g
δηλαδή είναι f g

● Εχουμε

● Α f Α g ={(- , 1] [2, + )} [2, + )=[2, + )
● f(x)= x -3x+2= (x-1)×(x-2)= x-1 x-2 g(x)
2
Συνεπώς
στο διάστημα [2, + ) έχουμε f(x)=g(x), δηλαδή f=g.

Τακης Τσακαλακος Κερκυρα 2017