Page 166 - olokliroma

166
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

Ε ν α λ λ α κ τ ι κ ά

Θεωρούμε τη συνάρτηση
με τύπο
h(x)=f(x)-g(x)=

= 2εφxσυνx-ημx
● Οι h είναι συνεχής στο
π 3π
διάστημα [ , ]
3 2
σαν πράξεις συνεχών
● Οι ρίζες της f(x)=0`

2εφxσυνx=0 είναι ρ=π
● Οι ρίζες της g(x)=0`
ημχ=0 είναι ρ=π
π 3π
● ρ [ , ]

3 2
3
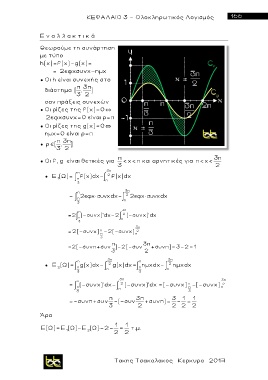
● Οι f, g είναι θετικές για < x< π και αρνητικές για π< x<
3 2
3π
π
● Ε (Ω)= f(x) dx- 2 f(x) dx
1 π π
3
3π
π
= 2 x dx- 2 2 x dx
π π
3
3π
π
= 2 (- συνx)' dx-2 2 (- συνx)' dx
π π
3
= 2[- συνx] π -2[- συνx] 3π
2
π π
3
π 3π
= 2[- συνπ+συν ]-2[- συν +συνπ]= 3-2= 1
3 2

π 3π π 3π
● Ε (Ω)= π g(x) dx- 2 g(x) dx= π ημx dx - 2 ημx dx
2
3 π 3 π
3π 3π
π
= π (- συνx)' dx- 2 (- συνx)' dx =[- συνx] π π -[- συνx] π 2
3 π 3
π 3π 3 1 1
=- συνπ+συν -(- συν +συνπ)= - =
3 2 2 2 2
Άρα

1 1
Ε(Ω) = Ε (Ω)-Ε (Ω) 2 2 = 2 τ.μ.
1
2

Τακης Τσακαλακος Κερκυρα 2017