Page 169 - olokliroma

169
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

Ε ν α λ λ α κ τ ι κ ά

Θεωρούμε τη συνάρτηση
με τύπο
h(x)=f(x)-g(x)=

=x -2x+2
2
● Οι f, g είναι συνεχείς
στο διάστημα [1, 3]
σαν πολυωνυμικές.
● Η εξίσωση x -2x+2=0 είναι
2
δ ε ν έχει ρίζες

● ρ [0, 3]
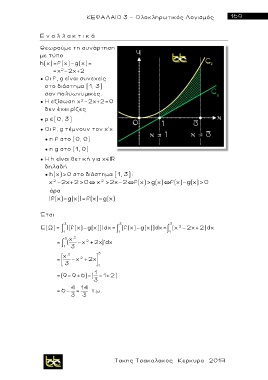
● Οι f, g τέμνουν τον χ'χ

● η f στο (0, 0)

● η g στο (1, 0)
● Η h είναι θετική για χ
δηλαδή
● h(x)>0 στο διάστημα [1, 3]:
x -2x+2 0` x 2 2x-2`f(x) g(x)` f(x)-g(x) 0
2
άρα
| f(x)-g(x)|=f(x)-g(x)

Έτσι

3 3 3
Ε(Ω) = |(f(x)-g(x)) | dx= (f(x)-g(x)) dx= (x -2x+2) dx
2
1 1 1
3 x 3
= ( -x 2 +2x )' dx
1 3
x 3 3
= -x 2 +2x
3 1

=(9-9 +6)-( 1 -1+2)
3

4 14
= 6- = τ.μ.
3 3

Τακης Τσακαλακος Κερκυρα 2017