Page 173 - olokliroma

173
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

2
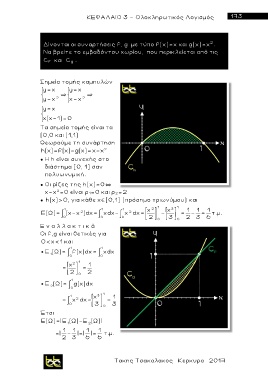
Δίνονται οι συναρτήσεις f, g με τύπο f(x)=x και g(x)=x .
Nα βρείτε το εμβαδόντου χωρίου, που περικλείεται από τις
C f και C g .

Σημεία τομής καμπυλών

y= x y= x
y= x 2 x= x 2

y= x

x(x-1)= 0

Τα σημεία τομής είναι τα

(0,0 και (1,1)
Θεωρούμε τη συνάρτηση

2
h(x)=f(x)-g(x)=x-χ

● Η h είναι συνεχής στο

διάστημα [0, 1] σαν
πολυωνυμική.

● Οι ρίζες της h(x)=0`

χ-x =0 είναι ρ 1=0 και ρ 2=2
2

● h(x)>0, για κάθε χ [0,1] (πρόσημο τριωνύμου) και
1 1 1 x 2 1 x 3 1 1 1 1
E(Ω) = (x-x ) dx= x dx- x dx= - = - = τ.μ.
2
2
0 0 0 2 0 3 0 2 3 6
E ν α λ λ α κ τ ι κ ά

Οι f,g είναι θετικές για

0<x<1 και
1 1

Ε (Ω)= f(x) dx x dx
1
0 0
2 1 1

2 0 2
1

Ε (Ω)= g(x) dx
2
0
1 3 1 1
= x dx=
2
0 3 0 3
Έτσι

Ε(Ω) = | Ε (Ω)- Ε (Ω)|
2
1

= | 1 - 1 |= | 1 |= 1 τ.μ.
2 3 6 6

Τακης Τσακαλακος Κερκυρα 2017