Page 230 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 230

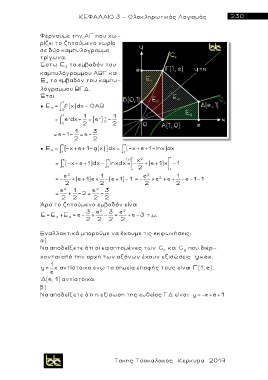
Φέρνουμε την ΑΓ που χω-
ρίζει το ζητούμενο χωρίο
σε δύο καμπυλογραμμα
τρίγωνα.
Έστω Ε το εμβαδόν του
3
καμπυλόγραμμου ΑΒΓ και
Ε το εμβαδόν του καμπυ-
4
λόγραμμου ΒΓΔ.
Έτσι
1
● Ε = f(x)dx- OAB
3
0
1 1 1
= e dx- =[e ] -
x
x 1
0 2 0 2

= e-1- 1 = e- 3
2 2
e e
● Ε = [ -x+e+1-g(x)] dx= (-x+e+1-lnx)dx
4
1 1
e e (γ) x 2 e
= (-x+e+1)dx- lnxdx = - +(e+1)x -1
1 1 2 1
e 2 1 e 2 1
2
=- +(e+1)e+ -(e+1)-1 =- +e +e+ -e-1-1
2 2 2 2
= e 2 + 1 -2= e 2 - 3
2 2 2 2
Άρα το ζητούμενο εμβαδόν είναι
3 e 2 3 e 2
Ε= Ε +Ε = e- 2 + 2 - 2 = 2 +e-3 τ.μ.
3
4

Εναλλακτικά μπορούμε να έχουμε τις εκφωνήσεις:
α )
Να αποδείξετε ότι οι εφαπτομένες των C και C που διέρ-
f g
χονται από την αρχή των αξόνων έχουν εξισώσεις y=ex,
1
y= x αντίστοιχα ενώ τα σημεία επαφής τους είναι Γ(1, e),
e
Δ(e, 1) αντίστοιχ α .
β )

Να αποδείξετε ότι η εξίσωση της ευθείας ΓΔ είναι: y x e 1

Τακης Τσακαλακος Κερκυρα 2017