Page 225 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 225

δ)
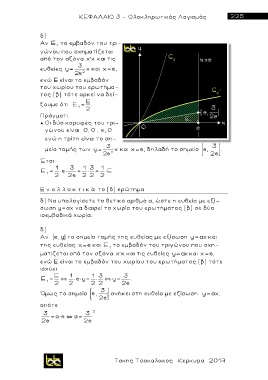
Αν Ε το εμβαδόν του τρι-
1
γώνου που σχηματίζεται
από τον αξόνα x x και τις
3
ευθείες y x και x e,
2e 2
ενώ Ε είναι το εμβαδόν
του χωρίου του ερωτήμα-
τος (β) τότε αρκεί να δεί-

ξουμε ότι Ε .
1 2
Πράγματι
● Ο ι δύο κορυφές του τρι-
γώνου είναι 0, 0 , e, 0
ενώ η τρίτη είναι το ση-

3 3
μείο τομής των y x και x e, δηλαδή το σημείο e, .
2e 2 2e
Έτσι
1 3 1 3 1
Ε 1 = 2 × e× 2e = 2 2 = 2 × Ε
×

Ε ν α λ λ α κ τ ι κ ά το (δ) ερώτημα

δ) Να υπολογίσετε το θετικό αριθμ ό α, ώστε η ευθεία με εξί-
σωση y=αχ να διαιρεί το χωρίο του ερωτήματος (β) σε δύο
ισεμβαδικά χωρία.

δ )
Αν (e, y ) το σημείο τομής της ευθείας με εξίσωση y=αx και
της ευθείας x e και Ε το εμβαδόν του τριγώνου που σχη -
1
ματίζεται από τον αξόνα x x και τις ευθείες y x και x e,

ενώ Ε είναι το εμβαδόν του χωρίου του ερωτήματος (β) τότε
ισχύει
Ε 1 1 3 3
×
Ε = 2 ` 2 × e× y= 2 2 ` y= 2e .
1
3
Όμως το σημείο e, ανήκει στη ευθεία με εξίσωση y=αx,
2e
οπότε
3 = α× e ` α= 3 2
2e 2e

Τακης Τσακαλακος Κερκυρα 2017