Page 224 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 224

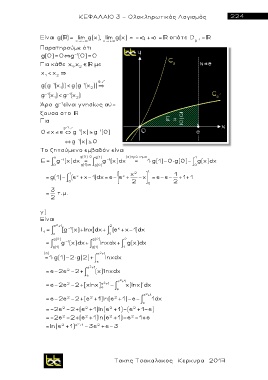
Είναι g( ) lim g(x), lim g(x) = , οπότε D
x - x + g 1
Παρατηρούμε ότι
-1
g(0)=0`g (0)=0
Για κάθε x , x με
1 2
x < x ~
2
1
g:
g(g (x ))< g(g (x )) ~
-1
-1
1 2
g (x )< g (x )
-1
-1
2
1
-1
Άρα g είναι γνησίως αύ-
ξουσα στο
Για
g 1 : <
1
1
0 x e g (x) g (0)

1
g (x) 0
Το ζητούμενο εμβαδόν είναι
e g(0) =0 g(1) (α) ερώτημα 1
-1
-1
Ε= g (x) dx = g (x) dx = 1× g(1)-0× g(0)- g(x) dx
0 g(1) =e g(0) 0
1 x 2 1 1
x
= g(1)- (e +x-1 ) dx= e- e + -x = e-e- +1+1
x
0 2 0 2
3
τ.μ.
2

γ)
Είναι
2
e +1 2
x
I = [g (x)+lnx] dx+ (e +x-1) dx
-1
1
e 1
g(2) g(2) 2
= g (x) dx+ lnx dx+ g(x) dx
-1
g(1) g(1) 1
(α) e +1
2
=1× g(1)-2× g(2)+ lnx dx
e
2
e +1
=e-2e -2+ (x)'lnx dx
2
e
2
e +1
=e-2e -2+[xlnx] e +1 - x(lnx)' dx
2
2
e
e
e +1
2
=e-2e -2+(e +1)ln(e +1)-e- 1 dx
2
2
2
e
2
=-2e -2+(e +1)ln(e +1)-(e +1-e)
2
2
2
=-2e -2+(e +1)ln(e +1)-e -1+e
2
2
2
2
2
2
=ln(e +1) e +1 -3e +e-3
2

Τακης Τσακαλακος Κερκυρα 2017