Page 227 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 227

f(1) = 0
f(e)=2e

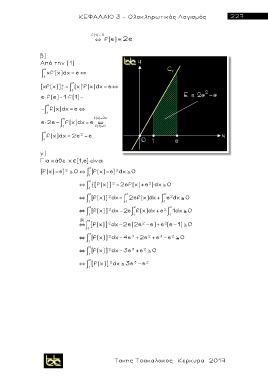
β)
Από την (1)
e
xf'(x)dx= e
1
e
[xf(x)] e (x)'f(x)dx= e `
1
1
e× f(e)-1× f(1)-
e
- f(x)dx= e
1
e f(e ) 2e
e× 2e- f(x)dx= e
1 f(1 ) 0
e
f(x)dx= 2e -e
2
1

γ)
Για κάθε x [1,e ] είναι
e
[f(x) e ] 2 0 [f(x) e ] dx 0
2
1
e
{[f(x)] -2ef(x)+e } dx 0
2
2
1
e e e
2
2
[f(x)] dx- 2ef(x)dx+ e dx 0
1 1 1
e e e
2
[f(x)] dx 2e f(x)dx e 2 1dx 0
1 1 1
( ) e
[f(x)] dx-2e(2e -e)+e (e-1) 0
2
2
2
1
e
[f(x)] dx-4e +2e +e -e 2 0
3
2
3
2
1
e
[f(x)] dx-3e +e 2 0
3
2
1
e
[f(x)] dx 3e -e
2
3
2
1

Τακης Τσακαλακος Κερκυρα 2017