Page 231 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 231

5. ΕΠΙΛΟΓΗ
Δίνεται η συνάρτηση f: (0, + ) με τύπο: f(x)=1+lnx
α ) Να αποδείξετε ότι η συνάρτηση f αντιστρέφεται και να
βρείτε την αντίστροφη της.

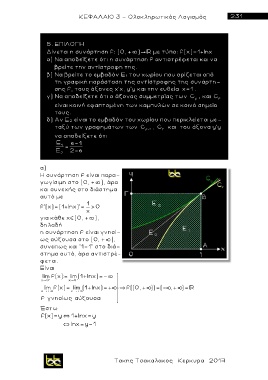
β ) Να βρείτε το εμβαδόν Ε 1 του χωρίου που ορίζεται από
τη γραφική παράσταση της αντίστροφης της συνάρτη-
σης f, του ς άξονε ς x'x, y'y και την ευθείa x=1 .
γ ) Να αποδείξετε ότι ο άξονας συμμετρίας των C f 1 και C
f
είναι κοινή εφαπτομένη των καμπυλών σε κοινό σημείο
τους.
δ) Αν Ε 2 είναι το εμβαδόν του χωρίου που περικλείεται με -
ταξύ των γραφημάτων των C 1 , C και του άξονα y'y
f f
να αποδείξετε ότι
Ε 1 = e-1
Ε 2 2-e

α )
Η συνάρτηση f είναι παρα-
γωγίσιμη στο (0, + ), άρα
και συνεχής στο διάστημα
αυτό με
1
f'(x)=(1+lnx)'= 0
x
για κάθε χ (0, + ),
δηλαδή
η συνάρτηση f είναι γνησί-
ως αύξουσα στο (0, + ),
συνεπως και "1-1" στο διά-
στημα αυτό, άρα αντιστρέ-
φεται.
Είναι

lim f(x) lim(1+lnx)
x 0 x 0
lim f(x) lim (1+lnx) ~ f((0, + )) (- , + )
x + x +
f γνησίως αύξουσα
Έστω
f(x)=y ` 1+lnx=y

` lnx=y-1

Τακης Τσακαλακος Κερκυρα 2017