Page 234 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 234

6. ΕΠΙΛΟΓΗ
1 t 2v 1
Δίνεται το ολοκλήρωμα 0 t 1 dx, ν ©*
α ) Να αποδείξετε ότι η παρασταση είναι ίση με
1
-1
(2v+3)(2v+2)
β ) Να βρείτε τα ολοκληρώματα Ι , Ι , Ι
1 2 3
Δίνεται η συνάρτηση f, συνεχής και παραγωγίσιμη για κάθε
πραγματικό αριθμό χ>0, για την οποία ισχύει
f(x+1)-f(x)= -1 , χ> 0
(2χ+3)(2χ+2)
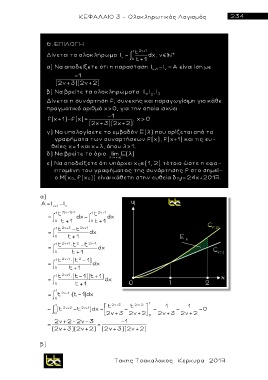
γ ) Να υπολογίσετε το εμβαδόν Ε(λ) που ορίζεται από τα
γραφήματα των συναρτήσεων f(x), f(x+1) και τις ευ-
θείες χ=1 και χ=λ, όπου λ>1.
δ) Να βρείτε το όριο lim Ε(λ)
λ + (1, 2) τέτοιο ώστε η εφα-
ε) Να αποδείξετε ότι υπάρχει χ 0
πτομένη του γραφήματος της συνάρτησης f στο σημεί-
ο Μ(χ 0, f(χ 0)) είναι κάθετη στην ευθεία δ:y=24x+2017.

α )
= Ι A Ι
ν+1 ν
1 t 2(v 1) 1 1 t 2v 1
dx dx
0 t 1 0 t 1

1 t 2v 3 t 2v 1
dx
0 t 1
1 t 2v 1 t 2 t 2v 1
dx
0 t 1
2
1 t 2v+1 ×(t -1)
= dx
0 t+1
1 t 2v+1 ×(t-1)(t+1)
= dx
0 t+1
1
t 2v 1 (t 1) dx
0
1 t 2v+3 t 2v+2 1 1 1
= (t 2v+2 -t 2v+1 ) dx 0
0 2v+3 2v+2 0 2v+3 2v+2
2v+2-2v-3 -1
= =
(2v+3)(2v+2) (2v+3)(2v+2)

β )

Τακης Τσακαλακος Κερκυρα 2017