Page 238 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 238

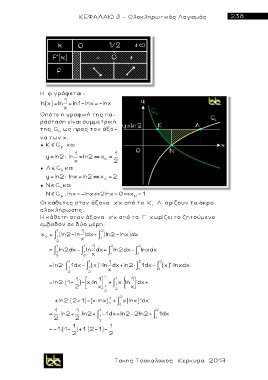
Η φ γράφεται :
1
h(x)= ln = ln1-lnx=-lnx
x
Οπότε η γραφική της πα-
ράσταση είναι συμμετρική
της C ως προς τον άξ ο -
h
να των x.
● K C και
φ
1 1
y ln2: ln ln2 x
x K 2
● C και
h
y ln2: lnx ln2 x 2
Λ
● C και
h
C : lnx=-lnx`2lnx= 0`x = 1
N
φ
Οι κάθετες στον άξονα x x α π ό τα K, Λ ορίζουν τα άκρα
ολοκλήρωσης.
Η κάθετη στον άξονα x x α π ό το Γ χωρίζει το ζητούμενο
εμβαδόν σε δύο μέρη.
1 1 2
x = (ln2-ln ) dx + (ln2-lnx) dx
0 1 x 1
2
1 1 1 2 2
= ln2 dx ln dx + ln2 dx lnx dx
1 1 x 1 1
2 2
1 1 1 2 2
= ln2× 1 dx - (x)' × ln dx +ln2× 1 dx - (x)' × lnx dx
1 1 x 1 1
2 2
= ln2×(1- 1 ) - x× ln 1 1 + 1 1 x× ln 1 ' dx+
1
2 x 2 2 x
+ln2×(2-1) - x× lnx 2 + 2 x(lnx) 'dx
1 1
1 1 1 2
= × ln2 + × ln2+ -1 dx +ln2 - 2ln2+ 1 dx
2 2 1 1
2
1 1
=- 1×(1- )+1×(2-1) =
2 2

Τακης Τσακαλακος Κερκυρα 2017