Page 242 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 242

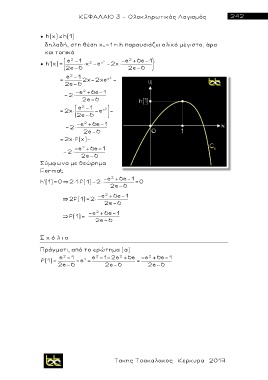
● h(x) h(1)
δηλαδή, στη θέση χ ο=1 η h παρουσιάζει ολικό μέγιστο, άρα

και τοπικό
2
e -1 2 -e +6e-1
2
● h'(x)= × χ -e x -2x '
2
2e-6 2e-6
e -1 2
2
= 2χ-2χe x -
2e-6
2
-2 -e +6e-1
2e-6
2
= 2χ× e -1 -e x 2 -
2e-6
2
-2 -e +6e-1
2e-6
= 2χ× f(x)-
-e +6e-1
2
-2
2e-6
Σύμφωνα με θεώρημα
Fermat
-e +6e-1
2
h'(1)=0~2 1 f(1)-2 =0
2e-6
-e +6e-1
2
~2f(1)=2
2e-6
-e +6e-1
2
~f(1)=
2e-6

Σ χ ό λ ι ο

Πράγματι, από το ερώτημα (α)
2
2
2
e -1 e -1-2e 2 6e -e +6e-1
f(1)= -e 1
2e-6 2e-6 2e-6

Τακης Τσακαλακος Κερκυρα 2017