Page 247 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 247

β )
Έχουμε
● Α f=
● f συνεχής στο

● f παραγωγίσιμη στο μ ε
f'(x)= e (x+1)
x
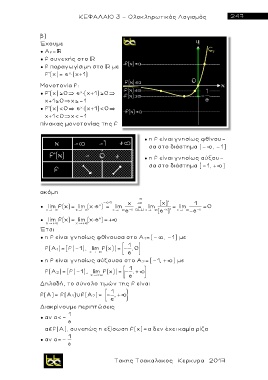
Μονοτονία f:
● f'(x) 0~ e (x+1) 0~
x
x+1 0~χ -1
● f'(x)<0~ e (x+1)<0~
x
x+1<0~χ<-1
πίνακας μονοτονίας της f

● η f είναι γνησίως φθίνου-
σα στο διάστημα (- , -1]

● η f είναι γνησίως αύξου-
σα στο διάστημα [-1, + )

ακόμη
-
- × 0 x (x)' 1
● lim f(x) lim (x e ) = lim lim lim 0
x
x
x - x - x - e x DLH x - (e )' x - -e x
● lim f(x) lim (x e )
x
x + x +
Έτσι
● η f είναι γνησίως φθίνουσα στο Α 1=(- , -1] μ ε
1
f(Α 1)=[f(-1), lim f(x))= - , 0
x - e
● η f είναι γνησίως αύξουσα στο Α 2=[-1, + ) με
1
f(Α 2)=[f(-1), lim f(x))= - , +
x = e
Δηλαδή, το σύνολο τιμών της f είναι
1
f(A)= f(Α 1) f(Α 2)= - , +
e
Διακρίνουμε περιπτώσεις
1
● αν α<-
e
α f(A), συνεπώς η εξίσωση f(x)=α δεν έχει καμία ρίζα
1
● αν α=-
e

Τακης Τσακαλακος Κερκυρα 2017