Page 250 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 250

11. ΕΠΙΛΟΓΗ
χ - y
2
t
Η εξίσωση 0 t e dt=1 παριστάνει μια γραμμή (c) στο ε-
πίπεδο.

α) Να απροσδιορίσετε τη συνάρτηση f που έχει γράφημα
τη γραμμή (c).
β ) Να υπολογίσετε το εμβαδόν του χωρίου που ορίζεται
από τα γρaφήματα των συναρτήσεων f και g(x)=3x-3.
Δίνεται επιπλέον η συνάρτηση h, συνεχής στο διάστημα
[0, π], για την οποία ισχύει 3π(π-2)h(x)=4g(x) και Η μια
αρχική της.
γ ) Να υπολογίσετε τον αριθμό Η(π)-Η ( 0)

δ) Να αποδείξετε ότι υπάρχει χ 0 (0, π) τέτοιο, ώστε
h(x 0)=ημχ 0.

α )
Έχουμε διαδοχικά
2
χ - y
t e dt 1`
t
0
2
χ - y
t (e )' dt 1`
t
0
χ - y
2
2
[te ] χ - y - (t)'e dt=1`
t
t
0
0
2
χ - y
2
( χ - y)e χ - y - e dt=1`
t
2
0
( χ - y)e χ - y -[e ] χ - y =1`
2
2
t
2
0
2
2
2
( χ - y)e χ - y -e χ - y +1= 1`
e χ 2 - y 0
2
( χ - y-1)e χ - y =0 `
2
χ - y-1=0 `
2
2
y=χ -1
2
χ - y
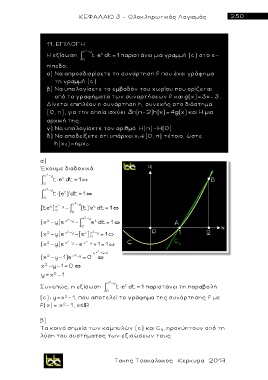
Συνεπώς, η εξίσωση t e dt 1 παριστάνει τη παραβολή
t
0
(c): y=x -1, που αποτελεί το γράφημα της συνάρτησης f μ ε
2
f(x)= x -1, x
2

β)
Τα κοινά σημεία των καμπυλών (c) και C g, προκύπτουν από τη
λύση του συστήματος των εξισώσεων τους

Τακης Τσακαλακος Κερκυρα 2017