Page 253 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 253

12. ΕΠΙΛΟΓΗ
1 e x
Δίνεται η συνάρτηση f:[0, + ) με f(x)= x ln e x

α) Να αποδείξετε ότι η συνάρτηση f αντιστρέφεται και να
βρείτε την αντίστροφη της.
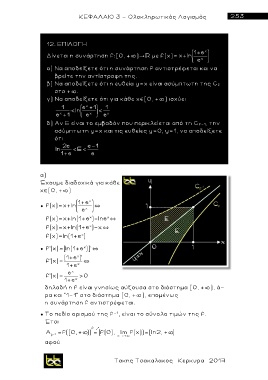
β ) Να αποδείξετε ότι η ευθεία y=x είναι ασύμπτωτη της C f
στο + .
γ ) Να αποδείξετε ότι για κάθε χ [0, + ) ισχύει
x
x 1 ln e x 1 1 x
e +1 e e
δ) Αν Ε είναι το εμβαδόν που περικλεί εται από τη C f - 1, την
ασύμπτωτη y=x και τις ευθείες y=0, y=1, να αποδείξετε
ότι
ln 2e E e 1
1+e e

α )
Έχουμε διαδοχικά για κάθε
χ [0, + )

1+e x
● f(x) x+ln `
e x

x
f(x) x+ln(1+e )-lne `
x
f(x) x+ln(1+e )-x`
x
x
f(x) ln(1+e )
x
● f'(x) [ln(1+e )]'`
(1+e )'
x
f'(x) `
1+e x
e x
f'(x) 0
1+e x

δηλαδή η f είναι γνησίως αύξουσα στο διάστημα [0, + ), ά-
ρα και "1-1" στο διάστημα [0, + ), επομένως
η συνάρτηση f αντιστρέφεται.

● Το πεδίο ορισμού της f - 1 , είναι το σύνολο τιμών της f.
Έτσι
f
Α f([0, + )) = [f(0), lim f(x))=[ln2, + )
f -1 x +
αφού

Τακης Τσακαλακος Κερκυρα 2017