Page 249 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 249

Έτσι
1 2017χ 2016 dχ 1 2017χ 2016 e x dχ

1 e 1 1 1+e
1 2017χ 2016 2017χ 2016 e x
dχ
1 1+e
x
1 2017χ 2016 (1 e )
dχ
1 1+e
1
2017χ 2016 dχ
1
Ι = Κ
[χ 2017 1 1 1 2 `
]
-1
2Ι=2`Ι=1

δ )
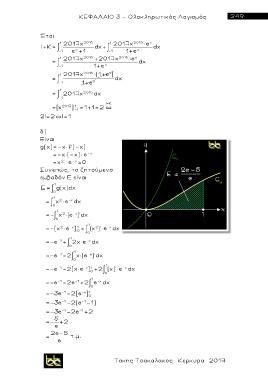
Είναι
g(x)=-χ f(-x)
=-χ (-χ ) e - χ
=χ e - χ 0
2
Συνεπώς, το ζητούμενο
εμβαδόν Ε είναι
1
Ε g(x) dχ
0
1
x 2 e dχ
x
0
1
x 2 (e )' dχ
x
0
1
-[x × e ] (x )' e dχ
-x 1
2
x
2
0
0
1
-e -1 2x× e dχ
-x
0
1
-e -1 2 x×(e )' dχ
-x
0
1
-e -1 2[x× e ] 2 (x)' × e dχ
-x 1
-x
0
0
1
-e -1 2e -1 2 e dχ
-x
0
-3 e -1 2[e ]
-x 1
0
-3e -1 2(e -1)
-1
-3e -1 2e -1 +2
5
- +2
e
2e-5
τ.μ.
e
Τακης Τσακαλακος Κερκυρα 2017