Page 246 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 246

10. ΕΠΙΛΟΓΗ
Δίνε τ αι η συνάρ τ ηση f με πεδ'ιο ορισμού το , για την οποία
ισχύει, για κάθε χ
● είναι συνεχής στο

● f(0)=0
● f'(x)-f(x)= e
x
α) Να αποδείξετε ότι f(x)= x e για κάθε χ
x
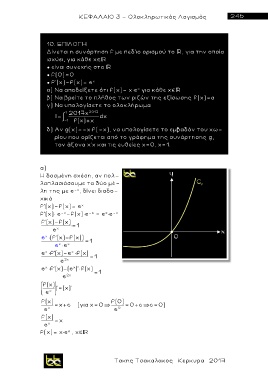
β ) Να βρείτε το πλήθος των ριζών της εξίσωσης f(χ)=α
γ ) Να υπολογίσετε το ολοκλήρωμα
1 2017χ 2017
1 f(x) dχ

δ) Αν g(x)=-x f(-x), να υπολογίσετε το εμβαδόν του χω-
ρίου που ορίζεται από το γράφημα της συνάρτησης g,
τον άξονα χ'χ και τις ευθείες χ=0, χ=1.

α )
Η δοσμένη σχέση, αν πολ-
λαπλασιάσουμε τα δύο μέ-
λη της με e - x , δίνει διαδο-
χικά
f'(x)-f(x)= e
x
f'(x) e - x -f(x) e - x = e e - x
x
f'(x)-f(x) 1

e x
e x (f'(x)-f( ))x 1
e x e x
e x f'(x)-e x f(x) 1
e 2x
x
e x f'(x)-(e )' f(x) 1
e 2x
f(x) ' =(x)'
e x
f(x) =x+c (για χ=0~ f(0) =0+c~ c=0)

e x e 0
f(x) = x
e x
f(x)= x e , χ
x

Τακης Τσακαλακος Κερκυρα 2017