Page 252 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 252

= h(x) dχ
0
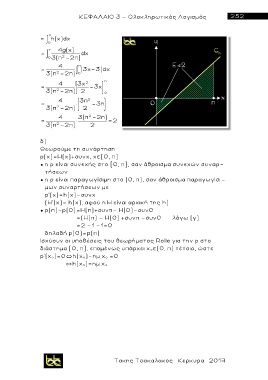
4g(x)
= dχ
0 3(π -2π)
2
4
= (3x-3) dχ
3(π -2π) 0
2

= 4 3x 2 -3χ π
2
3(π -2π) 2 0
4 3π 2
= -3π
3(π -2π) 2
2
4 3(π -2π)
2
= 2
3(π -2π) 2
2

δ )
Θεωρούμε τη συνάρτηση
p(x)=H(x)+συνχ, χ [0, π]
● η p είναι συνεχής στο [0, π], σαν άθροισμα συνεχών συναρ-

τήσεων
● η p είναι παραγωγίσιμη στο (0, π), σαν άθροισμα παραγωγίσι -
μων συναρτήσεων με
p'(x)=h(x)-συνχ
(Η'(χ)= h(χ), αφού η Η είναι αρχική της h)
● p(π)-p(0)=Η(π)+συνπ- Η(0)-συν0
=(Η(π) - Η(0) +συνπ -συν0 λόγω (γ)

=2 -1 -1=0
δηλαδή p(0)=p(π)
Ισχύουν οι υποθέσεις του θεωρήματος Rolle για την p στο
διάστημα [0, π], επομένως υπάρχει χ ο (0, π) τέτοιο, ώστε
p'(χ ο)=0`h(χ ο)-ημ χ ο =0
`h( χ ο)=ημ χ ο

Τακης Τσακαλακος Κερκυρα 2017