Page 237 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 237

7. ΕΠΙΛΟΓΗ
Δίνεται η συνάρτηση f(x)=x+x -lnx
2
α) Να αποδείξετε ότι η συνάρτηση f παρουσιάζει ελάχιστο

στη θέση x , όπου x είναι το εμβαδόν του χωρίου που
0
0
ορίζεται από τις γραφικές παραστάσεις των συναρτή-
1
σεων h(x)= lnx, φ(x)= ln και την ευθεία y=ln2,
x
το οποίο και να βρείτε.
2
Έστω g(x)=x -lnx και Α(x , g(x )), Β(x , g(x )) δυο διαφο-
1
2
1
2
ρετικά σημεία της γραφικής παράστασης της συνάρτησης
g.
β ) Να αποδείξετε ότι η y=x είναι εφαπτομένη της C g στο
σημείο της (1, g(1)) και στη συνέχεια ότι ισχύει
2 x 2 g(t)dt> x -x
2
2
x 1 2 1
γ ) Αν Ε είναι το εμβαδόν που ορίζεται από τη C , την y x
g
και τις ευθείες x=x , x=x να αποδείξετε ότι
x x 1 2
Ε> 2 f(x)dx-2 2 g(x)dx
x 1 x 1
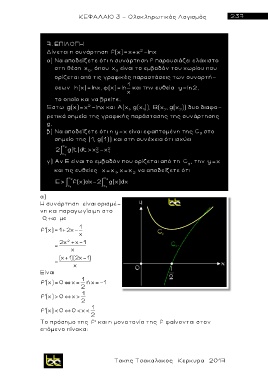
α )
Η συνάρτηση είναι ορισμέ-
νη και παραγωγίσιμη στο
0 , με

f'(x)= 1+2x 1
x
2x 2 x 1

x
(x 1 )(2x 1 )

x
Είναι
1
f'(x ) 0 x ή x 1
2
1
f'(x)> 0 x
2
1
f'(x) 0 0 x
2
Tο πρόσημο της f και η μονοτονία της f φαίνονται στον
επόμενο πίνακα:

Τακης Τσακαλακος Κερκυρα 2017