Page 239 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 239

1
Η συνάρτηση f παρουσιάζει ελάχιστο στο , με τιμή
2
1 3
f ln2
2 4

β)
Η εφαπτομένη της C στο σημείο της (1, g(1)), έχει εξίσωση:
g
g (1) = 1
y-g(1)= g'(1)× x-1 ` y= x
g(1) = 1
Η συνάρτηση g είναι κυρτή στο 0 , , αφού
1 1
g'(x)=(x -lnx)' = 2x- και g''(x)= 2+ >0, x 0,+ .
2
x x 2
Επομένως για κάθε x 0,+ θα ισχύει g(x) x, με την ισότητα
να ισχύει αν και μόνο αν x 1
Για κάθε t [x , x ] ισχύει
2
1
g(t)-t 0, με την ισότητα
να ισχύει το πολύ για μια
τιμή του t.
Επομένως
x 2
(g(t)-t)dt> 0`
x 1
x 2 x 2
g(t)dt> tdt `
x 1 x 1

x 2 t 2 x 2
g(t)dt> `
x 1 2 x 1
x 2
2 g(t)dt> x -x
2
2
x 1 2 1

γ )
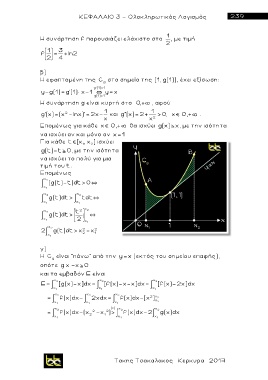
Η C είναι “πάνω” από την y x (εκτός του σημείου επαφής),
g
οπότε g x x 0

και το εμβαδόν Ε είναι
x 2 x 2 x 2
Ε = [g(x)-x]dx= [f(x)-x-x]dx= [f(x)-2x] dx
x 1 x 1 x 1
x 2 x 2 x 2
2
= f(x)dx- 2xdx= f(x)dx-[x ] x 2
x 1 x 1 x 1 x 1
x 2 (ε) x 2 x 2
= f(x)dx-(x 2 -x 2 )> f(x)dx-2 g(x)dx
x 1 2 1 x 1 x 1

Τακης Τσακαλακος Κερκυρα 2017