Page 222 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 222

3α 1
α 3 = 4α 3 3 1= 0 α= 1
4 4
αφού, από σχήμα Horner
4α 3 3 1= 0

(α 1 )(4α 2 4 1 ) 0
α > 0
(α 1 )(2 1 ) 2 0 α 1
2α +1 > 0

δ)
Είναι για a=1
● f x x , x 0 και
3
● f'(x) 3 x , x 0
2
3
2
● f'(x)-f(x)=3x -x
2
=x (3-x)>0
για x [ 0,1 ]
και
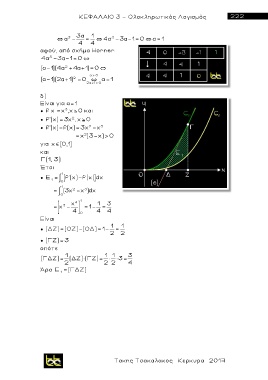
Γ(1, 3)
Έτσι

1
● Ε f'(x) f(x) dx
1
0
1
= (3x 2 x )dx
3
0
4 1
= x 3 x 1 1 3
4 0 4 4
Είναι
1 1
● (ΔΖ)=(ΟΖ)-(ΟΔ)= 1- =
2 2
● (ΓΖ)=3
οπότε
1
(ΓΔΖ)= (ΔΖ)×(ΓΖ)= 1 × 1 × 3= 3
2 2 2 4
Άρα Ε =(ΓΔΖ)
1

Τακης Τσακαλακος Κερκυρα 2017