Page 221 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 221

Ετσι
1 αx ν+2 1 1
E= (OAB) 1 = α x ν+2 v+2=4 v=2
2 v+2 2 2 1
Άρα η ζητούμενη συνάρτηση είναι η

f(x)=αx 3 , α>0, x 0

β)
Έχουμε
f'(x) 3 x >0, αφού α>0
2
άρα η συνάρτηση f είναι γνησίως αύξουσα στο πεδίο ορισμού
της.

γ)
f''(x) 6 x

x = 1
0
● f'(x )= 3α `(ε): y-3α= 6α(x-1)`(ε): y= 6αx-3α (1)
0
f''(x )= 6α
0
● Για y 0 η (1) δίνει
3 1
0 6 x 3 x
6 2
1
Το σημείο Δ , 0 είναι το
2
σημείο τομής της (ε) και
του άξονα χ'χ.
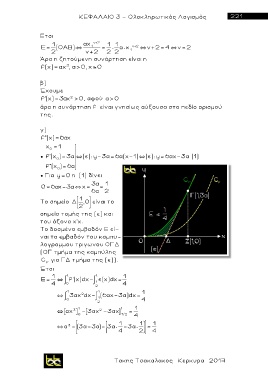
Το δοσμένο εμβαδόν Ε εί-

ναι το εμβαδόν του καμπυ-
λογραμμου τριγωνου ΟΓΔ
(ΟΓ τμήμα της καμπύλης
C για ΓΔ τμήμα της (ε)).
f'
Έτσι
1 1 1 1
Ε= f'(x)dx ε(x)dx=
4 0 1 4
2
1 1 1
3αx dx (6αx 3α)dx=
2
0 1 4
2
αx 3 1 3αx 2 3αx 1 = 1
0 1/2 4

α 3 (3α 3α) 3α 1 3α 1 = 1
4 2 4

Τακης Τσακαλακος Κερκυρα 2017