Page 5 - TEYXOS_A

1.3. ΘΕΩΡΙΑ 87

Γραφική παράσταση της f και της αντίστροφης συνάρτησης

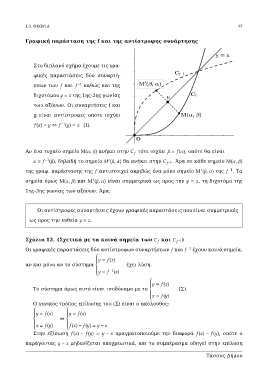
Στο διπλανό σχήμα έχουμε τις γρα-
φικές παραστάσεις δύο συναρτή-

σεων των και − καθώς και της

διχοτόμου = της 1ης-3ης γωνίας
των αξόνων. Οι συναρτήσεις f και

g είναι αντίστροφες οπότε ισχύει

−
() = ⇔ () = (1).

Αν ένα τυχαίο σημείο Μ(, ) ανήκει στην τότε ισχύει = (), οπότε θα είναι

−
′
= (), δηλαδή το σημείο (, ) θα ανήκει στην −. Άρα σε κάθε σημείο Μ( , )

′
−
της γραφ. παράστασης της αντιστοιχεί ακριβώς ένα μόνο σημείο Μ (, ) της . Τα
′
σημεία όμως Μ(, ) και Μ (, ) είναι συμμετρικά ως προς την = , τη διχοτόμο της
1ης-3ης γωνίας των αξόνων. Άρα:

Οι αντίστροφες συναρτήσεις έχουν γραφικές παραστάσεις που είναι συμμετρικές
ως προς την ευθεία = .

Σχόλιο 12. (Σχετικά με τα κοινά σημεία των και −)

Οι γραφικές παραστάσεις δύο αντίστροφων συναρτήσεων και − έχουν κοινά σημεία,
⎧
⎪
⎪
⎪
⎪ = ()
⎨
αν και μόνο αν το σύστημα ⎪ έχει λύση.
⎪ −
⎪
⎪
⎩ = ()
⎧
⎪
⎪
⎪
⎪ = ()
⎨
Το σύστημα όμως αυτό είναι ισοδύναμο με το ⎪ (Σ).
⎪
⎪
⎪
⎩ = ()
Ο γενικός τρόπος επίλυσης του (Σ) είναι ο ακόλουθος:
⎧
⎧
⎪ ⎪
⎪
⎪
⎪
⎪
⎪ = ()
⎪ = ()
⎨
⎨
⎪ ⇔ ⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩() − () = −
⎩ = ()
Στην εξίσωση () − () = − πραγματοποιούμε την διαφορά () − (), οπότε ο
παράγοντας − μηδενίζεται υποχρεωτικά, και το συμπέρασμα οδηγεί στην επίλυση
Τάσσος Δήμου