Page 106 - 01 Einstein
P. 106
coordenadas. Los puntos 1 y 2 están a distancias diferentes según
las midamos desde A o desde B, pero la distancia entre ellos no
cambia. En lenguaje algebraico se dice que la distancia es un inva-
riante (figura ll). A partir de la métrica se puede calcular cual-
LA PUESTA EN PIE DE LA MÉTRICA
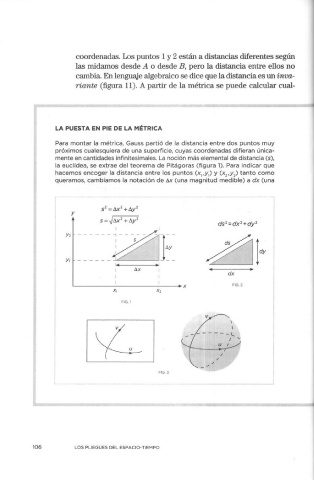
Para montar la métrica, Gauss partió de la distancia entre dos puntos muy
próximos cualesquiera de una superficie, cuyas coordenadas difieran única-
mente en cantidades infinitesimales. La noción más elemental de distancia (s),
la euclídea, se extrae del teorema de Pitágoras (fig ura 1). Para indicar que
hacemos encoger la distancia entre los puntos (x ,y ) y (x ,y ) tanto como
1 1 2 2
queramos, cambiamos la notación de t:,.x (una magnitud medible) a dx (una
52 = M2 +óy2
y
s = ,jt:,.x2 + óy2
/!,X
dx
~--------------. x FIG.2
x, X2
FIG.1
V
- - - - - - -1...
/ 1 '
U 1
/
--/
FIG. 3
106 LOS PLIEGUES DEL ESPACIO-TIEMPO