Page 102 - 01 Einstein

La condición extrema que
hemos impuesto a estos trazados
los distingue del resto de posibles
trayectorias, haciendo que merez-
can un nombre propio: geodésicas.
No importa cuánto compliquemos
la geografía de la superficie; se-
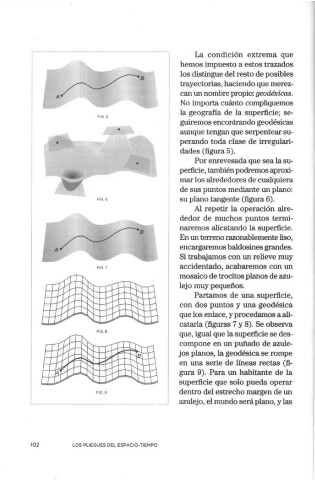
FIG. 5
guiremos encontrando geodésicas
aunque tengan que serpentear su-
perando toda clase de irregulari-
dades (figura 5).
Por enrevesada que sea la su-
perficie, también podremos aproxi-
mar los alrededores de cualquiera
de sus puntos mediante un plano:
FIG. 6 su plano tangente (figura 6).
Al repetir la operación alre-
dedor de muchos puntos termi-
naremos alicatando la superficie.
En un terreno razonablemente liso,
encargaremos baldosines grandes.
Si trabajamos con un relieve muy
FIG. 7 accidentado, acabaremos con un
mosaico de trocitos planos de azu-
lejo muy pequeños.
Partamos de una superficie,
con dos puntos y una geodésica
que los enlace, y procedamos a ali-
catarla (figuras 7 y 8). Se observa
FIG. 8
que, igual que la superficie se des-
compone en un puñado de azule-
jos planos, la geodésica se rompe
en una serie de líneas rectas (fi-
gura 9). Para un habitante de la
superficie que solo pueda operar
FIG. 9 dentro del estrecho margen de un
L. azulejo, el mundo será plano, y las

102 LOS PLIEGUES DEL ESPACIO-TIEMPO