Page 100 - 20 Euclides

esta forma usando tángram; nosotros
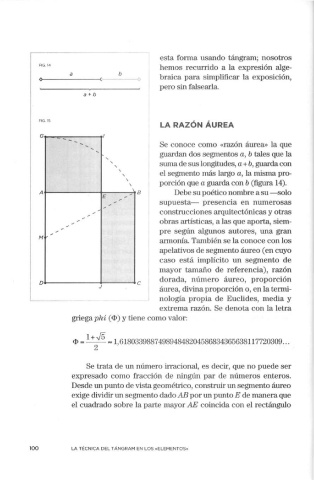
FIG. 14
hemos recurrido a la expresión alge-
a b
braica para simplificar la exposición,
pero sin falsearla.
a+b

FIG. 15
LA RAZÓN ÁUREA
G-------.
Se conoce como «razón áurea» la que
guardan dos segmentos a, b tales que la
' suma de sus longitudes, a+ b, guarda con
'
' \ el segmento más largo a, la misma pro-
\
porción que a guarda con b (figura 14).
A Debe su poético nombre a su - solo
E
supuesta- presencia en numerosas
/, construcciones arquitectónicas y otras
obras artísticas, a las que aporta, siem-
pre según algunos autores, una gran
armonía. También se la conoce con los
apelativos de segmento áureo ( en cuyo
caso está implícito un segmento de
mayor tamaño de referencia), razón
o-------J----c dorada, número áureo, proporción
áurea, divina proporción o, en la termi-
nología propia de Euclides, media y
extrema razón. Se denota con la letra
griega phi ( <I>) y tiene como valor:

<1> = l + .J5 = 1, 6180339887 49894848204586834365638117720309 ...
2

Se trata de un número irracional, es decir, que no puede ser
expresado como fracción de ningún par de números enteros.
Desde un punto de vista geométrico, construir un segmento áureo
exige dividir un segmento dado AB por un punto E de manera que
el cuadrado sobre la parte mayor AE coincida con el rectángulo

100 LA TÉCNICA DEL TÁNGRAM EN LOS «ELEMENTOS»