Page 103 - 27 Leibniz
P. 103
La medidaBQ corresponde a y,
y por tanto, como el triángulo ABQ
es semejante al triángulo caracterís- !
tico, tenemos que se cumple que
de donde
dy = dx
y e
e integrando esa expresión
X
ln(y) = -
e
y, por tanto, las curvas de subtan- L-
gente constante son las de expre-
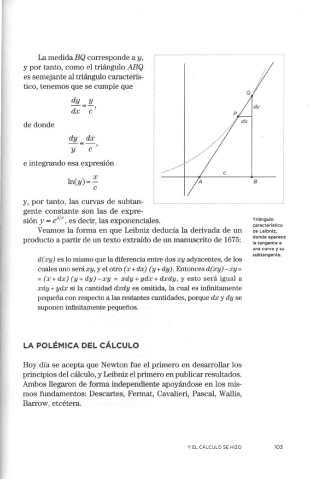
sión y= ex/e, es decir, las exponenciales. Triángulo
característico
Veamos la forma en que Leibniz deducía la derivada de un de Leibniz,
producto a partir de un texto extraído de un manuscrito de 1675: donde aparece
la tangente a
una curva y su
subtangente.
d( xy) es lo mismo que la diferencia entre dos xy adyacentes, de los
cuales uno seráxy, y el otro (x+dx) (y+dy). Entonces d(X'IJ) - xy=
= (x + dx) (y+ dy)-xy = xdy + ydx + dxdy, y esto será igual a
xdy + ydx si la cantidad dxdy es omitida, la cual es infinitamente
pequeña con respecto a las restantes cantidades, porque dx y dy se
suponen infinitamente pequeños.
LA POLÉMICA DEL CÁLCULO
Hoy día se acepta que Newton fue el primero en desarrollar los
principios del cálculo, y Leibniz el primero en publicar resultados.
Ambos llegaron de forma independiente apoyándose en los mis-
mos fundamentos: Descartes, Fermat, Cavalieri, Pascal, Wallis,
Barrow, etcétera.
Y EL CÁLCULO SE HIZO 103