Page 52 - 11 Gauss

jos y las implicaciones que podían tener en el futuro. La cuestión a
la que también respondió Gauss era: ¿necesitaremos los matemá-
ticos crear nuevos números para cada nueva ecuación que apa-
4
rezca?, ¿y si quisiéramos resolver una ecuación como x + 1 = O,
tendríamos que buscar nuevos números para resolverla? Gauss
probó que no era necesario: usando el número i, los matemáticos
podrían resolver cualquier ecuación polinómica que se les pusie-
ra por delante. Las soluciones eran una combinación de los habi-
tuales números reales y de este nuevo número i. Gauss descubrió
que los números imaginarios no eran más que añadir una nueva
dimensión a la habitual recta de los reales, por lo que cada número
imaginario corresponde a un punto en el plano, al igual que cada
número real corresponde a un punto de la recta. Además, Gauss
creó una nueva forma de representarlos mediante un eje de coor-
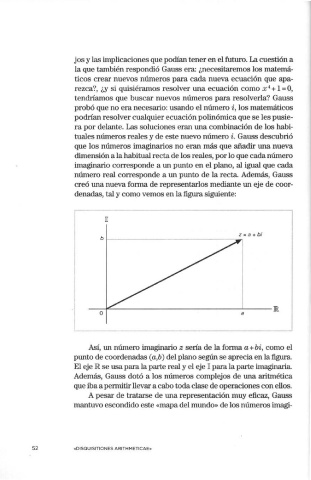
denadas, tal y como vemos en la figura siguiente:

,- - II

z =a+ bi
1 b t------------------,...,

1

1 o a
l

Así, un número imaginario z sería de la forma a+ bi, como el
punto de coordenadas ( a,b) del plano según se aprecia en la figura.
El eje lR se usa para la parte real y el eje Il para la parte imaginaria.
Además, Gauss dotó a los números complejos de una aritmética
que iba a permitir llevar a cabo toda clase de operaciones con ellos.
A pesar de tratarse de una representación muy eficaz, Gauss
mantuvo escondido este «mapa del mundo» de los números imagi-

52 «DISQUISITIONES ARITHMETICAE»