Page 97 - 02 Newton

rendada entre, primero, los conceptos de fluente y fluxión con en-
tidad propia, como elementos de una temía, con unas reglas algo-
rítmicas de fácil uso para calcular la fluxión de una fluente y, luego,
los diversos ejemplos de problemas que permiten resolver. Esa di-
ferenciación entre los elementos abstractos de la teoria y sus apli-
caciones a una ingente variedad de problemas es lo que permite
atribuir a Newton -y a Leibniz- el descubrimiento del cálculo.

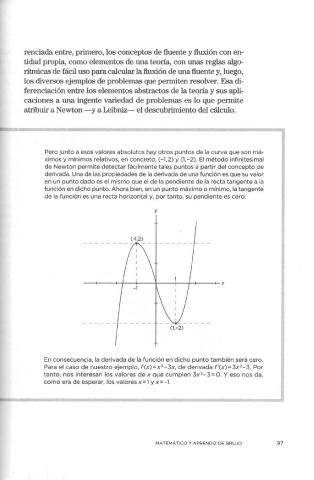
Pero junto a esos valores absolutos hay otros puntos de la curva que son má-
ximos y mínimos relativos, en concreto, (-1, 2) y (1, -2). El método infinitesimal
de Newton permite detectar fácilmente tales puntos a partir del concepto de
derivada. Una de las propiedades de la derivada de una función es que su valor
en un punto dado es el mismo que el de la pendiente de la recta tangente a la
función en dicho punto. Ahora bien, en un punto máximo o mínimo, la tangente
de la función es una recta horizontal y, por tanto, su pendiente es cero:
y

(1,- 2)

En consecuencia, la derivada de la función en dicho punto también será cero.
3
Para el caso de nuestro ejemplo, f(x)=x -3x, de derivada f'(x)=3x -3. Por
2
tanto, nos interesan los valores de x que cumplen 3x 2 - 3 = O. Y eso nos da,
como era de esperar, los valores x= 1 y x = -1.

MATEMÁTICO Y APRENDIZ DE BRUJO 97