Page 29 - Microsoft Word - 270 bai tap boi duong hoc sinh gioi toan 9doc.doc

WWW.MATHVN.COM MAI TRỌNG MẬU

a
a 2 + b c ³ 2 a 2 . b c = 2. = a Þ a 2 ³ a - b c
+
+
+
b c 4 b c 4 2 b c 4 .
+
+
+
b 2 a c c 2 a b
+
+
Tương tự : ³ b - ; ³ c - .
a c 4 a b 4
+
+
a 2 b 2 c 2 a b c a b c
+
+
+
+
Cộng từng vế 3 bất đẳng thức : + + ³ (a b c+ + ) - =
b c c a a b 2 2
+
+
+
2
2
2
2
2
2
2
Cách 2 : Theo BĐT Bunhiacôpxki : (a + b + c )(x + y + z ) ≥ (ax + by + cz) . Ta có :
é æ a ö 2 æ b ö 2 æ c ö 2 ù é 2 2 2 ù
+
+
+
+
+
ê ç ÷ + ç ÷ + ç ÷ ú X ê ( b c ) ( c a ) ( a b ) ú ≥
+
+
+
ë è ê b c ø è c a ø è a b ø ú ë û
û
æ a b c ö 2
+
+
+
≥ ç . b c + . c a + . a b ÷
+
+
+
è b c c a a b ø
æ a 2 b 2 c 2 ö a 2 b 2 c 2 a b c
+
+
Þ ç + + ÷ [ . 2(a b c)+ + ] (a b c)³ + + 2 Þ + + ³ .
+
+
+
+
+
+
è b c c a a b ø b c c a a b 2
x y
+
112. a) Ta nhìn tổng a + 1 dưới dạng một tích 1.(a + 1) và áp dụng bđt Cauchy : xy £
2
(a 1) 1 a
+
+
a 1 = 1.(a 1) £ = + 1
+
+
2 2
b c
Tương tự : b 1 = + 1 ; c 1 = + 1
+
+
2 2
a b c
+
+
Cộng từng vế 3 bất đẳng thức : a 1 + b 1 + c 1 £ + 3 3,5 .
+
=
+
+
2
Dấu “ = ” xảy ra Û a + 1 = b + 1 = c + 1 Û a = b = c = 0, trái với giả thiết a + b + c = 1.
+
<
+
+
Vậy : a 1 + b 1 + c 1 3,5.
b) Áp dụng bất đẳng thức Bunhiacôpxki với hai bộ ba số :
( 1. a b 1. b c 1. c a ) 2 £ (1 1 1)X é ( a b ) ( b c ) ( c a ) 2 ù Þ
2
2
+
+
+
+
+
+
+
+
+
+
+
+
ú
ê
ë
û
( a b + b c + c a ≤ 3(a + b + b + c + c + a) = 6Þ a b + b c + c a £ 6
)
2
+
+
+
+
+
+
C
B b
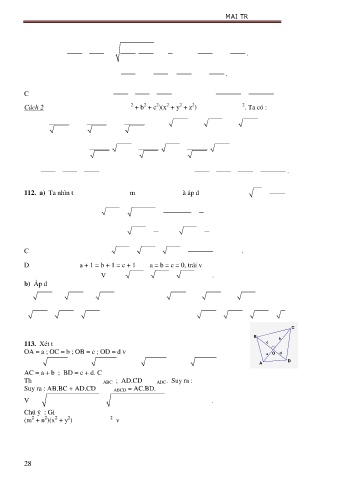
113. Xét tứ giác ABCD có AC ^ BD, O là giao điểm hai đường chéo. c
OA = a ; OC = b ; OB = c ; OD = d với a, b, c, d > 0. Ta có : a O d
AB = a + c ; BC = b + c ; AD = a + d ; CD = b + d A D
2
2
2
2
2
2
2
2
AC = a + b ; BD = c + d. Cần chứng minh : AB.BC + AD.CD ≥ AC.BD.
Thật vậy ta có : AB.BC ≥ 2S ABC ; AD.CD ≥ 2S ADC. Suy ra :
Suy ra : AB.BC + AD.CD ≥ 2S ABCD = AC.BD.
2
2
2
2
+
+
Vậy : (a + c 2 )( b + c 2 ) + (a + d 2 )( b + d 2 ) ³ (a b)(c d).
Chú ý : Giải bằng cách áp dụng bất đẳng thức Bunhiacôpxki :
2
2
2
2
2
(m + n )(x + y ) ≥ (mx + ny) với m = a , n = c , x = c , y = b ta có :
28 www.MATHVN.com