Page 127 - tmp

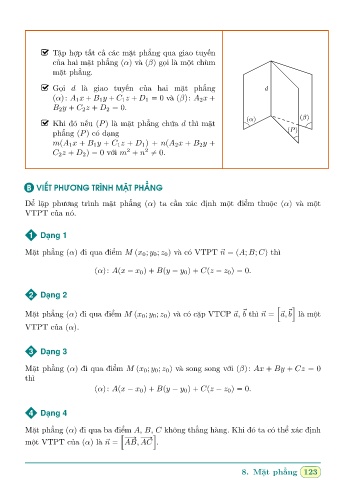
Tªp hñp t§t c£ các m°t ph¯ng qua giao tuy¸n
cõa hai m°t ph¯ng pαq và pβq gåi là mët chùm
m°t ph¯ng.
Gåi d là giao tuy¸n cõa hai m°t ph¯ng d
pαq: A 1 x B 1 y C 1 z D 1 0 và pβq: A 2 x
B 2 y C 2 z D 2 0.
pαq pβq
Khi đó n¸u pPq là m°t ph¯ng chùa d thì m°t
ph¯ng pPq có d¤ng pPq
mpA 1 x B 1 y C 1 z D 1 q npA 2 x B 2 y
2
C 2 z D 2 q 0 vîi m 2 n 0.

B VIẾT PHƯƠNG TRÌNH MẶT PHẲNG
Đº lªp phương trình m°t ph¯ng pαq ta c¦n xác đành mët điºm thuëc pαq và mët
VTPT cõa nó.

1 Dạng 1

M°t ph¯ng pαq đi qua điºm M px 0 ; y 0 ; z 0 q và có VTPT ~n pA; B; Cq thì

pαq: Apx x 0 q Bpy y 0 q Cpz z 0 q 0.

2 Dạng 2

~
~
M°t ph¯ng pαq đi qua điºm M px 0 ; y 0 ; z 0 q và có c°p VTCP ~a, b thì ~n ~a, b là mët
VTPT cõa pαq.
3 Dạng 3

M°t ph¯ng pαq đi qua điºm M px 0 ; y 0 ; z 0 q và song song vîi pβq: Ax By Cz 0
thì
pαq: Apx x 0 q Bpy y 0 q Cpz z 0 q 0.

4 Dạng 4
M°t ph¯ng pαq đi qua ba điºm A, B, C không th¯ng hàng. Khi đó ta có thº xác đành

ÝÝÑ ÝÑ
mët VTPT cõa pαq là ~n AB, AC .

8. M°t ph¯ng 123