Page 6 - geometria

Geometría 5° UNI

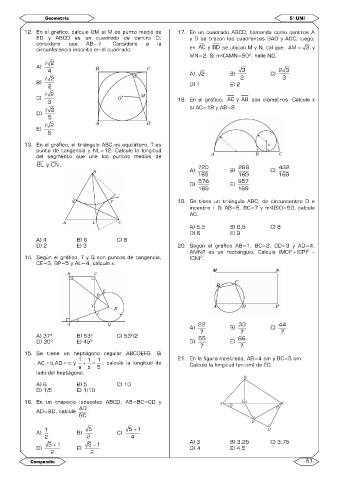
12. En el gráfico, calcule OM si M es punto medio de 17. En un cuadrado ABCD, tomando como centros A
ED y ABCD es un cuadrado de centro O; y D se trazan los cuadrantes BAD y ADC; luego,
considere que AB=  . Considere a la  
circunferencia inscrita en el cuadrado. en AC y BD se ubican M y N, tal que, AM = 3 y
MN=2. Si mAMN=90º, halle ND.
 2
A)
4 A) 2 B) 3 C) 23
 2 2 3
B) D) 1 E) 2
2
 2
C) 18. En el gráfico, AC y AB son diámetros. Calcule x
3
 2 si AC=18 y AB=8.
D)
5
 2
E)
6

13. En el gráfico, el triángulo ABC es equilátero, T es
punto de tangencia y NL=12. Calcule la longitud
del segmento que une los puntos medios de

BL y CN. 720 288 432
A) B) C)
169 169 169
576 657
D) E)
169 169

19. Se tiene un triángulo ABC, de circuncentro O e
incentro I. Si AB=5, BC=7 y mBIO=90, calcule
AC.

A) 5,5 B) 6,5 C) 8
D) 6 E) 9
A) 4 B) 6 C) 8
D) 2 E) 3 20. Según el gráfico AB=1, BC=2, CD=3 y AD=4,
AMNP es un rectángulo. Calcule (MC) +(CP) –
2
2
14. Según el gráfico, T y Q son puntos de tangencia, (CN) .
2
CE=3, BP=5 y AL=4, calcule x.

22 33 44
A) 7 B) 7 C) 7
A) 37º B) 53º C) 53º/2 55 66
D) 30º E) 45º D) E)
7 7
15. Se tiene un heptágono regular ABCDEFG. Si
1 1 1 21. En la figura mostrada, AB=4 cm y BC=5 cm.
AC = b,AD = c y + = , calcule la longitud de Calcule la longitud (en cm) de EC.
a b 5
lado del heptágono.

A) 6 B) 5 C) 10
D) 1/5 E) 1/10

16. En un trapecio isósceles ABCD, AB=BC=CD y
AD
AD=BD, calcule .
BC

1 5 5 + 1
A) B) C)
2 2 4
−
5 + 1 5 1 A) 3 B) 3,25 C) 3,75
D) E) D) 4 E) 4,5
2 2
Compendio -51-