Page 20 - KIII - Geometría 4

Geometría 4° Secundaria

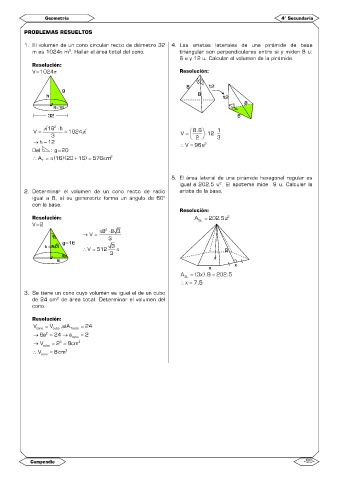
PROBLEMAS RESUELTOS

1. El volumen de un cono circular recto de diámetro 32 4. Las aristas laterales de una pirámide de base
m es 1024 m . Hallar el área total del cono. triangular son perpendiculares entre sí y miden 8 u;
3
6 u y 12 u. Calcular el volumen de la pirámide.
Resolución:
V=1024 Resolución:

16  h
2
V   1024   8.6 12 1
3 V    2    3
 h  12
 V  96u 3
Del : g=20



2

 A    16 20 16  576 m
T

5. El área lateral de una pirámide hexagonal regular es
2
igual a 202,5 u . El apotema mide 9 u. Calcular la
2. Determinar el volumen de un cono recto de radio arista de la base.
igual a 8, si su generatriz forma un ángulo de 60°
con la base.
Resolución:
Resolución: A SL  202.5u
2
V=2
2

 8 8 3
 V 
3
3
 V  512 
3

A SL   3x .9   202.5
 x  7,5

3. Se tiene un cono cuyo volumen es igual al de un cubo
2
de 24 cm de área total. Determinar el volumen del
cono.

Resolución:
V cono  V cubo ,siA Tcubo  24
 6a  24  a cubo  2
2
3
 V  2  8cm 3
cubo
 V  8cm 3
cono

Compendio -99-