Page 211 - KM Matematika_BS_KLS_IX

Contoh 3 Pada gambar berikut ini ΔABC merupakan segitiga siku-siku sama kaki. Tentukan panjang
sisi AB.

Penyelesaian
Karena AB : AC = 1 : 2 dan kita misalkan A

AB = x cm, x | = 1 | 2
6
2
2 x = 6 45 o 6 cm
6 1
x = x cm
2
= 32
45 o
Maka, AB = 32 cm Jawab: 32 cm C BAB 7 | Theorema Pythagoras
B

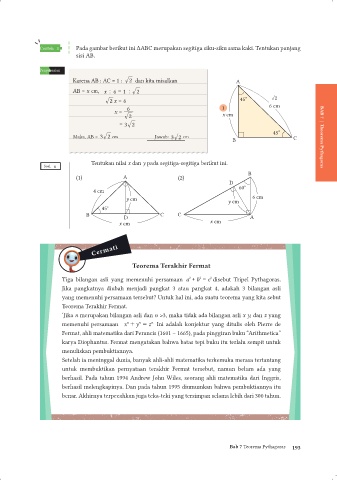
Tentukan nilai x dan y pada segitiga-segitiga berikut ini.
Soal 6
B
(1) A (2)
D
4 cm 60°
y cm y cm 6 cm
45°
B D C C A
x cm x cm

Cermati

Teorema Terakhir Fermat

2
Tiga bilangan asli yang memenuhi persamaan a + b = c disebut Tripel Pythagoras.
2
2
Jika pangkatnya diubah menjadi pangkat 3 atau pangkat 4, adakah 3 bilangan asli
yang memenuhi persamaan tersebut? Untuk hal ini, ada suatu teorema yang kita sebut
Teorema Terakhir Fermat.
‘Jika n merupakan bilangan asli dan n ≥3, maka tidak ada bilangan asli x y, dan z yang
n
n
n
memenuhi persamaan x + y = z Ini adalah konjektur yang ditulis oleh Pierre de
Fermat, ahli matematika dari Perancis (1601 – 1665), pada pinggiran buku “Arithmetica”
karya Diophantus. Fermat mengatakan bahwa batas tepi buku itu terlalu sempit untuk
menuliskan pembuktiannya.
Setelah ia meninggal dunia, banyak ahli-ahli matematika terkemuka merasa tertantang
untuk membuktikan pernyataan terakhir Fermat tersebut, namun belum ada yang
berhasil. Pada tahun 1994 Andrew John Wiles, seorang ahli matematika dari Inggris,
berhasil melengkapinya. Dan pada tahun 1995 diumumkan bahwa pembuktiannya itu
benar. Akhirnya terpecahkan juga teka-teki yang tersimpan selama lebih dari 300 tahun.

Bab 7 Teorema Pythagoras 193