Page 89 - KM Matematika_BS_KLS_IX

2
Tujuan Menyelesaikan persamaan kuadrat dengan mengubah ke dalam bentuk (x + p) = q

Isilah dengan bilangan yang memenuhinya.

2
(1) x + 8x + = (x + ) 2 (2) x - 6x + = (x – ) 2
2

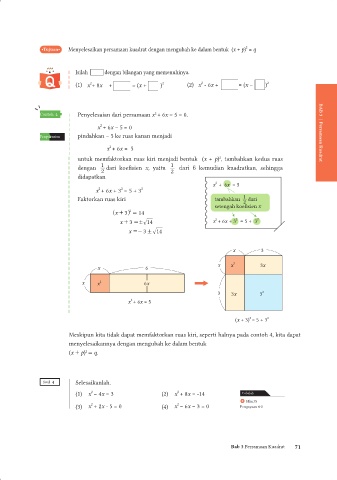
Contoh 4 Penyelesaian dari persamaan x + 6x – 5 = 0.
2
x + 6x – 5 = 0
2
Penyelesaian pindahkan – 5 ke ruas kanan menjadi BAB 3 | Persamaan Kuadrat

2
x + 6x = 5
untuk memfaktorkan ruas kiri menjadi bentuk (x + p) , tambahkan kedua ruas
2
dengan 1 dari koefisien x, yaitu 1 dari 6 kemudian kuadratkan, sehingga
2
didapatkan 2
x + 6x = 5
2
2
x + 6x + 3 = 5 + 3 2
2
Faktorkan ruas kiri tambahkan 1 2 dari
setengah koefisien x
3 =
] x + g 2 14
2
2
x + = ! 14 x + 6x + 3 = 5 + 3 2
3
x =- 3 ! 14
x 3

x 6 x x 2 3x

x x 2 6x
3 3x 3 2
x + 6x = 5
2

(x + 3) = 5 + 3 2
2
Meskipun kita tidak dapat memfaktorkan ruas kiri, seperti halnya pada contoh 4, kita dapat
menyelesaikannya dengan mengubah ke dalam bentuk
(x + p) = q.
2

Soal 4 Selesaikanlah.
(1) x – 4x = 3 (2) x + 8x = -14 Cobalah
2
2
Hlm.78
2
2
(3) x + 2x - 5 = 0 (4) x – 6x – 3 = 0 Pengayaan 4-2
4

Bab 3 Persamaan Kuadrat 71