Page 6 - HS 5 Spreidingsgetallen met oefeningen

Statistiek in de tweede graad

5.4.2 Vuistregel voor het bepalen van uitschieters

Je kan uiteraard niet zomaar op je intuïtie afgaan, om te besluiten of een getal een uitschieter is.
Hiervoor gebruik je in de statistiek de volgende vuistregel:

Stap 1: Bepaal het eerste kwartiel Q1 en ook het derde kwartiel Q3

Stap 2: Bepaal de interkwartielafstand IQR = Q3 – Q1
Het is gekend dat 50% van de resultaten hiertussen gelegen zijn.

Stap 3: Voor waarden die als «uitzonderlijk groot» worden bestempeld, neem je Q3 en tel je daar nog
anderhalf keer de interkwartielafstand bij.

Voor «uitzonderlijk klein» neem je alle getallen die gelegen zijn vóór Q1 verminderd met anderhalf keer
de interkwartielafstand.

Getallen die buiten [ Q1 - 1,5 x IQR, Q3 + 1,5 x IQR] gelegen zijn noemt men uitschieters.

Voorbeeld

Voor {1,8, 9,10,10,11,12,12,13,14,15,18,19,30 } is Q1 = 10 en Q3 = 15.
De interkwartielafstand IRQ = Q3 – Q1 = 15 – 10 = 5.

Q1 - 1,5 x IRQ = 10 – 7,5 = 2,5

Q3 + 1,5 x IRQ = 15 + 7,5 = 22,5
De getallen 1 en 30 zijn uitschieters.

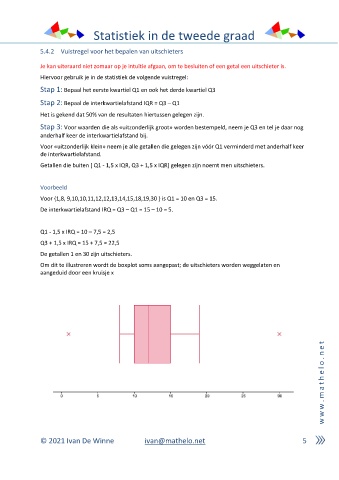
Om dit te illustreren wordt de boxplot soms aangepast; de uitschieters worden weggelaten en
aangeduid door een kruisje x

t
e
n
.
o
l
e
h
t
a
m
.
w

w
w

© 2021 Ivan De Winne ivan@mathelo.net 5