Page 159 - 수학(상)

개 념 01 평행이동

. 1 평행이동

좌표평면 위의 한 점 또는 도형을 일정한 방향으로 일정한 거리만큼 옮기는 것을 평행이동이라 한다.

2. 점의 평행이동

,
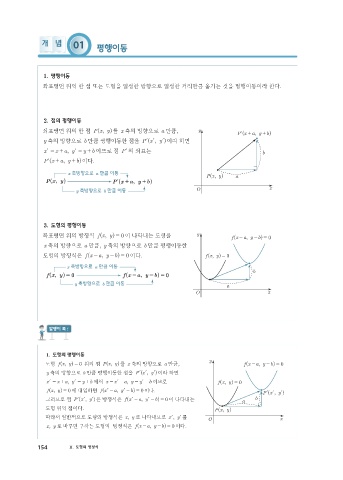
좌표평면 위의 한 점 P xyh 를 x 축의 방향으로 a 만큼, y P x + , a y + bh
^
l^
y 축의 방향으로 b 만큼 평행이동한 점을 P xl , ylh 이라 하면
l^
l
l
x =+ , ay =+ 이므로 점 Pl의 좌표는 b
y
b
x
P x + , a y + bh 이다.
l^
x 축방향으로 a 만큼 이동
P^ , xyh a
P^ , xyh P x + , a y + bh
l^
y 축방향으로 b 만큼 이동 O x

3. 도형의 평행이동
0
,
좌표평면 위의 방정식 f xy = 이 나타내는 도형을 y f x - , a y - h 0
h
^
b =
^
P
x 축의 방향으로 a 만큼, y 축의 방향으로 b 만큼 평행이동한
도형의 방정식은 f x - , a y - h 0 f^ , xy = 0
b = 이다.
^
h
x 축방향으로 a 만큼 이동
b
b =
h
f^ , xy = 0 f x - , a y - h 0
^
y 축방향으로 b 만큼 이동 a
O x
알맹이 콕 !

. 1 도형의 평행이동
y
,
,
b =
0
^
^
h
도형 f xy = 위의 점 P xyh 를 x 축의 방향으로 a 만큼, f x - , a y - h 0
^
y 축의 방향으로 b 만큼 평행이동한 점을 P xl , ylh 이라 하면
l^
l
x
x =+ , ay =+ 에서 x = l , ay = l b f^ , xy = 0
y
b
x -
l
y - 이므로
h
l
l
0
b =
f^ , xy = 에 대입하면 f x - , a y - h 0 이다. P xl , ylh
^
h
l^
l
그러므로 점 P xl , ylh 은 방정식은 f x - , a y - h 0 이 나타내는 a b
l
b =
l^
^
도형 위의 점이다. P^ , xyh
따라서 일반적으로 도형의 방정식은 ,xy 로 나타내므로 xl , yl를 O x
, xy 로 바꾸면 구하는 도형의 방정식은 f x - , a y - h 0
^
b = 이다.
154 Ⅲ . 도형의 방정식