Page 161 - 수학(상)

개 념 02 대칭이동

. 1 대칭이동

) 1 대칭이동
좌표평면 위의 도형을 한 점 또는 한 직선에 대하여 대칭인 도형으로 옮기는 것을
각각 그 점 또는 그 직선에 대한 대칭이동이라 한다.
180c 회전시킨다.
C Al
) 2 점대칭 Bl
점대칭은 도형을 어떤 점을 중심으로 180c회전시켰을 때, D
Dl
본래의 도형에 완전히 겹쳐지는 것을 말한다.
B
이때 그 점을 대칭의 중심이라 한다. A Cl
대칭의 중심

3) 선대칭 D
C 대칭축
선대칭은 어떤 도형을 한 직선을 중심으로 대칭시켰을 때,
겹쳐지는 것을 말한다. 즉 어떤 도형이 한 직선을 중심으로
A B
선대칭이라는 것은 이 직선을 접는 선으로 하여 접었을 때, Cl
완전히 겹쳐진다는 것을 뜻한다. Bl
미술에서 데칼코마니는 선대칭의 일종이다.
Dl

Al
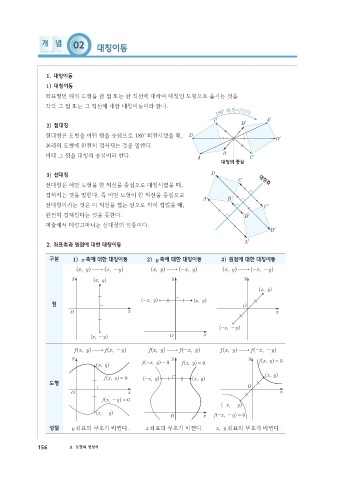
2. 좌표축과 원점에 대한 대칭이동

구분 ) 1 x 축에 대한 대칭이동 ) 2 y 축에 대한 대칭이동 ) 3 원점에 대한 대칭이동
h
^
^
^ , xy $ ^ , x - yh ^ , xy $ - , xyh ^ , xy $ - , x - yh
h
h
y y y
^ , xyh
^ , xyh
^ - , xyh ^ , xyh
점 O
O x x
^ - , x - yh

^ , x - yh O x
f -
f -
h
f^ , xy $ f^ , x - yh f^ , xy $ ^ , xyh f^ , xy $ ^ , x - yh
h
h
y y y
h
f - , xy = 0 f^ , xy = 0 f^ , xy = 0
h
^
h
^ , xyh
^ , xyh
h
f^ , xy = 0 ^ - , xyh ^ , xyh
도형
O
O x x
y =
f^ , x - h 0
^ - , x - yh
^ , x - yh
y =
O x f - , x - h 0
^
성질 y 좌표의 부호가 바뀐다. x 좌표의 부호가 바뀐다. , xy 좌표의 부호가 바뀐다.
156 Ⅲ . 도형의 방정식