Page 44 - علم الأوبئة

‫ﻋﻠﻢ اﻷوﺑﺌﺔ‬

‫‪٠٫١٦‬‬

‫‪٠٫١٤‬‬

‫‪٠٫١٢‬‬

‫‪٠٫١‬‬

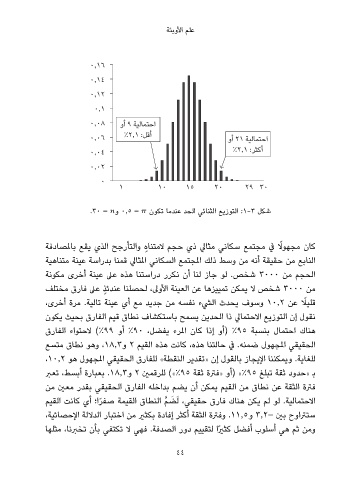
‫اﺣﺘﻤﺎﻟﻴﺔ ‪ ٩‬أو ‪٠٫٠٨‬‬ ‫اﺣﺘﻤﺎﻟﻴﺔ ‪ ٢١‬أو‬
‫أﻗﻞ‪٠٫٠٦ ٪٢٫١ :‬‬ ‫أﻛﺜﺮ‪٪٢٫١ :‬‬

‫‪٠٫٠٤‬‬

‫‪٠٫٠٢‬‬

‫‪٠١‬‬ ‫‪١٠ ١٥ ٢٠ ٢٩ ٣٠‬‬

‫ﺷﻜﻞ ‪ :1-3‬اﻟﺘﻮزﻳﻊ اﻟﺜﻨﺎﺋﻲ اﻟﺤﺪ ﻋﻨﺪﻣﺎ ﺗﻜﻮن ‪ ٠٫٥ = π‬و‪.٣٠ = n‬‬

‫ﻛﺎن ﻣﺠﻬﻮ ًﻻ ﰲ ﻣﺠﺘﻤﻊ ﺳﻜﺎﻧﻲ ﻣﺜﺎﱄ ذي ﺣﺠﻢ ﻻﻣﺘﻨﺎ ٍه واﻟﺘﺄرﺟﺢ اﻟﺬي ﻳﻘﻊ ﺑﺎلمﺼﺎدﻓﺔ‬
‫اﻟﻨﺎﺑﻊ ﻣﻦ ﺣﻘﻴﻘﺔ أﻧﻪ ﻣﻦ وﺳﻂ ذﻟﻚ المﺠﺘﻤﻊ اﻟﺴﻜﺎﻧﻲ المﺜﺎﱄ ﻗﻤﻨﺎ ﺑﺪراﺳﺔ ﻋﻴﻨﺔ ﻣﺘﻨﺎﻫﻴﺔ‬
‫اﻟﺤﺠﻢ ﻣﻦ ‪ ٣٠٠٠‬ﺷﺨﺺ‪ .‬ﻟﻮ ﺟﺎز ﻟﻨﺎ أن ﻧﻜﺮر دراﺳﺘﻨﺎ ﻫﺬه ﻋﲆ ﻋﻴﻨﺔ أﺧﺮى ﻣﻜﻮﻧﺔ‬
‫ﻣﻦ ‪ ٣٠٠٠‬ﺷﺨﺺ ﻻ ﻳﻤﻜﻦ ﺗﻤﻴﻴﺰﻫﺎ ﻋﻦ اﻟﻌﻴﻨﺔ اﻷوﱃ‪ ،‬ﻟﺤﺼﻠﻨﺎ ﻋﻨﺪﺋ ٍﺬ ﻋﲆ ﻓﺎرق ﻣﺨﺘﻠﻒ‬
‫ﻗﻠﻴ ًﻼ ﻋﻦ ‪ ١٠٫٢‬وﺳﻮف ﻳﺤﺪث اﻟﴚء ﻧﻔﺴﻪ ﻣﻦ ﺟﺪﻳﺪ ﻣﻊ أي ﻋﻴﻨﺔ ﺗﺎﻟﻴﺔ‪ .‬ﻣﺮة أﺧﺮى‪،‬‬
‫ﻧﻘﻮل إن اﻟﺘﻮزﻳﻊ اﻻﺣﺘﻤﺎﱄ ذا اﻟﺤﺪﻳﻦ ﻳﺴﻤﺢ ﺑﺎﺳﺘﻜﺸﺎف ﻧﻄﺎق ﻗﻴﻢ اﻟﻔﺎرق ﺑﺤﻴﺚ ﻳﻜﻮن‬
‫ﻫﻨﺎك اﺣﺘﻤﺎل ﺑﻨﺴﺒﺔ ‪) ٪٩٥‬أو إذا ﻛﺎن المﺮء ﻳﻔﻀﻞ‪ ٪٩٠ ،‬أو ‪ (٪٩٩‬ﻻﺣﺘﻮاء اﻟﻔﺎرق‬
‫اﻟﺤﻘﻴﻘﻲ المﺠﻬﻮل ﺿﻤﻨﻪ‪ .‬ﰲ ﺣﺎﻟﺘﻨﺎ ﻫﺬه‪ ،‬ﻛﺎﻧﺖ ﻫﺬه اﻟﻘﻴﻢ ‪ ٢‬و‪ ،١٨٫٣‬وﻫﻮ ﻧﻄﺎق ﻣﺘﺴﻊ‬
‫ﻟﻠﻐﺎﻳﺔ‪ .‬وﻳﻤﻜﻨﻨﺎ اﻹﻳﺠﺎز ﺑﺎﻟﻘﻮل إن »ﺗﻘﺪﻳﺮ اﻟﻨﻘﻄﺔ« ﻟﻠﻔﺎرق اﻟﺤﻘﻴﻘﻲ المﺠﻬﻮل ﻫﻮ ‪،١٠٫٢‬‬
‫ﺑ »ﺣﺪود ﺛﻘﺔ ﺗﺒﻠﻎ ‪) «٪٩٥‬أو »ﻓﱰة ﺛﻘﺔ ‪ («٪٩٥‬ﻟﻠﺮﻗﻤين ‪ ٢‬و‪ .١٨٫٣‬ﺑﻌﺒﺎرة أﺑﺴﻂ‪ ،‬ﺗﻌﱪ‬
‫ﻓﱰة اﻟﺜﻘﺔ ﻋﻦ ﻧﻄﺎق ﻣﻦ اﻟﻘﻴﻢ ﻳﻤﻜﻦ أن ﻳﻀﻢ ﺑﺪاﺧﻠﻪ اﻟﻔﺎرق اﻟﺤﻘﻴﻘﻲ ﺑﻘﺪر ﻣﻌين ﻣﻦ‬
‫اﻻﺣﺘﻤﺎﻟﻴﺔ‪ .‬ﻟﻮ ﻟﻢ ﻳﻜﻦ ﻫﻨﺎك ﻓﺎرق ﺣﻘﻴﻘﻲ‪َ ،‬ﻟ َﻀ ﱠﻢ اﻟﻨﻄﺎق اﻟﻘﻴﻤﺔ ﺻﻔ ًﺮا؛ أي ﻛﺎﻧﺖ اﻟﻘﻴﻢ‬
‫ﺳﺘﱰاوح ﺑين ‪ ٣٫٢−‬و‪ .١١٫٥‬وﻓﱰة اﻟﺜﻘﺔ أﻛﺜﺮ إﻓﺎدة ﺑﻜﺜير ﻣﻦ اﺧﺘﺒﺎر اﻟﺪﻻﻟﺔ اﻹﺣﺼﺎﺋﻴﺔ‪،‬‬
‫وﻣﻦ ﺛﻢ ﻫﻲ أﺳﻠﻮب أﻓﻀﻞ ﻛﺜي ًرا ﻟﺘﻘﻴﻴﻢ دور اﻟﺼﺪﻓﺔ‪ .‬ﻓﻬﻲ ﻻ ﺗﻜﺘﻔﻲ ﺑﺄن ﺗﺨﱪﻧﺎ‪ ،‬ﻣﺜﻠﻬﺎ‬

‫‪44‬‬