Page 131 - Untitled
P. 131
מתמטיקה ,תשע"ב ,מועד ב ,מס' + 317 ,035807נספח .5
الرياضيات ،2012 ،الموعد "ب" ،رقم + 317 ،035807ملحق
معطاة الدالة f(x) = (x2 - a)e-0.5x2المع َّرفة لك ّل a .xهو بارامتر.
أ (1) .هل الدالة ) f(xهي زوجية أم فردية؟ ع ّلل.
) (2هل دالة المشت ّقة ) f'(xهي زوجية أم فردية؟ ع ّلل.
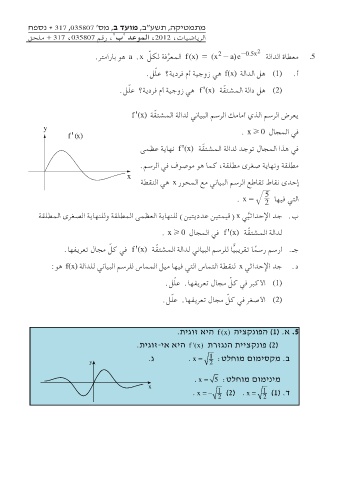
يعرض الرسم الذي أمامك الرسم البياني لدالة المشت ّقة )f'(x
y في المجال . xH0
)f' (x في هذا المجال توجد لدالة المشت ّقة ) f'(xنهاية عظمى
مطلقة ونهاية صغرى مطلقة ،كما هو موصوف في الرسم.
إحدى نقاط تقاطع الرسم البياني مع المحور xهي النقطة x
=. x 5 التي فيها
2
ب .جد الإحداث َّيي ( xقيمتين عدديتين) للنهاية العظمى المطلقة وللنهاية الصغرى المطلقة
لدالة المشت ّقة ) f'(xفي المجال . xH0
جـ .ارسم رس ًما تقريب ًّيا للرسم البياني لدالة المشت ّقة ) f'(xفي ك ّل مجال تعريفها.
د .جد الإحداثي xلنقطة التماس التي فيها ميل المماس للرسم البياني للدالة ) f(xهو:
) (1الأكبر في ك ّل مجال تعريفها .ع ّلل.
) (2الأصغر في ك ّل مجال تعريفها .ع ّلل.
.5א (1) .הפונקציה ) f(xהיא זוגית.
) (2פונקציית הנגזרת ) f '(xהיא אי-זוגית.
y ג. =.x 1 ב .מקסימום מוחלט:
2
מינימום מוחלט. x = 5 :
x .x= − 1 )(2 =.x 1 ד(1) .
2 2