Page 13 - E-modul Fisika Matematika Materi Kalkulus Variasi_Neat
P. 13
2 ̇
( , , ) = √ + . Jelas terlihat bahwa = 0 dan = ̇ . Subsitusikan
̇
̇
√ + 2 ̇
hasil tersebut ke persamaan Euler (14) diperoleh ( ̇ ) = 0 atau
√ + ̇ 2
̇
(i)
√ + ̇ 2
Dimana c adalah sebuah konstanta. Bentuk persamaan (i) dapat diubah
2 ̇
2
2
menjadi ( − ) = , sehingga diperoleh:
2
= (ii)
2
√ − 2
Integrasikan persamaan (ii) diperoleh = ∫ + =
2
√ − 2
−
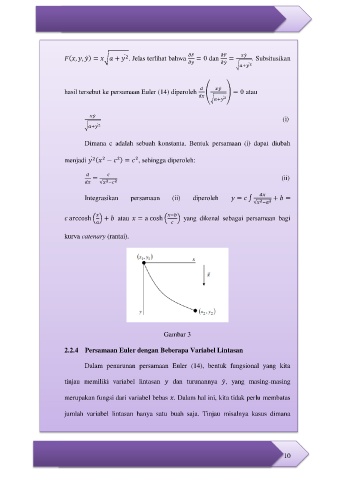
arccosh ( ) + atau = a cosh ( ) yang dikenal sebagai persamaan bagi
kurva catenary (rantai).
Gambar 3
2.2.4 Persamaan Euler dengan Beberapa Variabel Lintasan
Dalam penurunan persamaan Euler (14), bentuk fungsional yang kita
tinjau memiliki variabel lintasan dan turunannya , yang masing-masing
̇
merupakan fungsi dari variabel bebas . Dalam hal ini, kita tidak perlu membatas
jumlah variabel lintasan hanya satu buah saja. Tinjau misalnya kasus dimana
10