Page 66 - 12 Kepler

.. . .... -· rocosos (Mercurio, Venus, Tierra
dientes a los planetas internos o
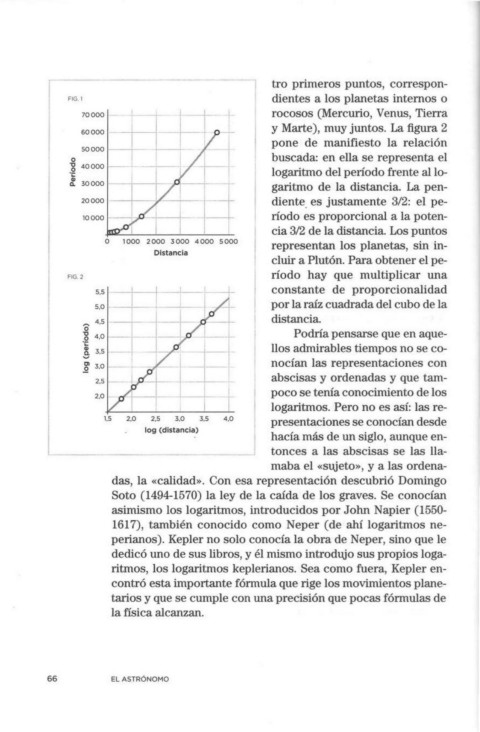
FIG. l tro primeros puntos, correspon-
70000 ffl···· ·+t ¡··
60 000 1 ! -· y Marte), muy juntos. La figura 2
pone de manifiesto la relación
so 000 1 ········ - .. .. ! . ·-
] 4ºººº ___ L _ . -- buscada: en ella se representa el
ai 1 logaritmo del período frente al lo-
a. 30 000 1----i---+-~ :---+----i
garitmo de la distancia. La pen-
diente_ es justamente 3/2: el pe-
ríodo es proporcional a la poten-
cia 3/2 de la distancia. Los puntos
O 1000 2000 3000 4000 5000
representan los planetas, sin in-
Distancia
cluir a Plutón. Para obtener el pe-
ríodo hay que multiplicar una
FIG. 2
constante de proporcionalidad
por la raíz cuadrada del cubo de la
distancia.
~ 4,5 1---,--
0
] 4,0 ,--..;- Podría pensarse que en aque-
ai llos admirables tiempos no se co-
S 3,5
nocían las representaciones con
abscisas y ordenadas y que tam-
poco se tenía conocimiento de los
logaritmos. Pero no es así: las re-
1,5 2,0 2,5 3,0 3,5 4,0
presentaciones se conocían desde
log (distancia)
hacía más de un siglo, aunque en-
tonces a las abscisas se las lla-
maba el «sujeto», y a las ordena-
das, la «calidad». Con esa representación descubrió Domingo
Soto (1494-1570) la ley de la caída de los graves. Se conocían
asimismo los logaritmos, introducidos por John Napier (1550-
1617), también conocido como Neper (de ahí logaritmos ne-
perianos). Kepler no solo conocía la obra de Neper, sino que le
dedicó uno de sus libros, y él mismo introdujo sus propios loga-
ritmos, los logaritmos keplerianos. Sea como fuera, Kepler en-
contró esta importante fórmula que rige los movimientos plane-
tarios y que se cumple con una precisión que pocas fórmulas de
la física alcanzan.

66 EL AS.TRÓNOMO