Page 137 - Bahan Ajar Metode Statistika
P. 137
BAB VI
SEBARAN NORMAL
A. Pendahuluan
Peubah acak kontinu dan fungsi kepekatannya muncul bila data
percabaan kita didefinisikan pada suatu ruang contoh yang kontinu. Oleh
karena itu, bila kita mengukur selang waktu, bobot, tinggi, volume, dan
lainnya, maka populasi kita nyatakan dengan suatu sebaran kontinu. Seperti
juga terdapat beberapa sebaran peluang diskrit yang khusus. Kita mengenal
banyak sekali sebaran kontinu, yang grafiknya menunjukkan kemenjuluran
atau dalam beberapa kasus setangkup sempurna. Di antara semua itu, yang
sejauh ini paling penting adalah suatu sebaran kintinu yang grafiknya
berbentuk geenta dan menjulur takterbatas pada kedua arah. Sebaran ini
yang merupakan landasan bagi sebagian besar teori inferensia statistik.
B. Kurva Normal
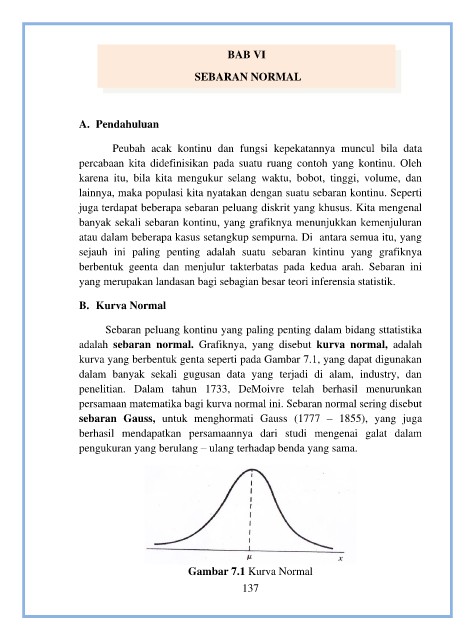
Sebaran peluang kontinu yang paling penting dalam bidang sttatistika
adalah sebaran normal. Grafiknya, yang disebut kurva normal, adalah
kurva yang berbentuk genta seperti pada Gambar 7.1, yang dapat digunakan
dalam banyak sekali gugusan data yang terjadi di alam, industry, dan
penelitian. Dalam tahun 1733, DeMoivre telah berhasil menurunkan
persamaan matematika bagi kurva normal ini. Sebaran normal sering disebut
sebaran Gauss, untuk menghormati Gauss (1777 – 1855), yang juga
berhasil mendapatkan persamaannya dari studi mengenai galat dalam
pengukuran yang berulang – ulang terhadap benda yang sama.
Gambar 7.1 Kurva Normal
137