Page 184 - analysinew

184
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

4. ΟΡIΟ (ΑΠΟΛΥΤΗ ΤΙΜΗ - ΑΠΡΟΣΔΙΟΡΙΣΤΙΑ 0 )
0
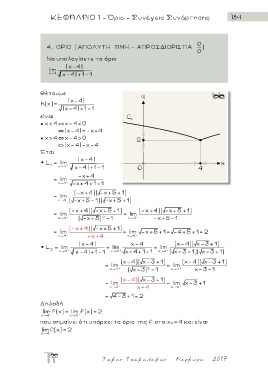
Να υπολογίσετε το όριο
| x- 4|
lim | x- 4| + 1-1
x 4

Θέτουμε
| x- 4|
h(x)=
| x- 4| + 1-1
είναι
● χ<4`χ-4<0
`|χ-4|=-χ+4
● χ>4`χ-4>0
`|χ-4|=χ-4
Έτσι
L lim | x- 4|
1 x 4 - | x- 4| + 1-1

-x+4
= lim
x 4 - -x+4+1-1
(-x+4)( -x+5 +1)
= lim
x 4 - ( -x+5-1)( -x+5 +1)
(- x+4)( - x+5 +1) (- x+4)( - x+5 +1)
= lim = lim
2
x 4 - ( - x+5) -1 x 4 - - x+5-1
(- x+4) ( - x+5 +1)
= lim = lim - x+5 +1= - 4+5 +1 = 2
x 4 - - x+ 4 x 4 -
L lim | x- 4| = lim x-4 = lim (x-4)( x-3 +1)
2
x 4 + | x- 4| + 1-1 x 4 + x-4+1-1 x 4 + ( x-3-1)( x-3 +1)

(x-4)( x-3 +1) (x-4)( x-3 +1)
= lim = lim
2
x 4 + ( x-3) -1 x 4 + x-3-1
(x-4) ( x-3 +1)
= lim = lim x-3 +1
x 4 + x-4 x 4 +
= 4-3 +1 = 2
Δηλαδή
lim f(x)= lim f(x)= 2
x 4 - x 4 +
που σημαίνει ότι υπάρχει το ό ρ ι ο της f στο χ 0=4 και είναι
limf(x)=2
x 4

Τακης Τσακαλακος Κερκυρα 2017