Page 124 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 124

2. ΓΕΩΜΕΤΡΙΑ
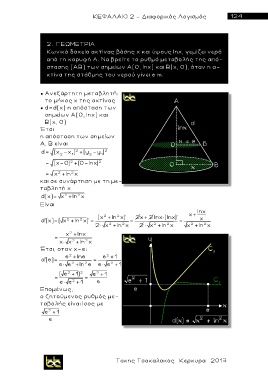
Κωνικό δοχείο ακτίνας βάσης χ και ύψους lnx, γεμίζει νερό
α π ό τη κορυφή Α. Να βρείτε το ρυθμό μεταβολής της από-
στασης (ΑΒ) των σημείων Α(0, lnx) και Β(χ, 0), όταν η α-
κτίνα της στάθμης του νερού γίνει e m.

● Ανεξάρτητη μεταβλητή:
το μήκ ο ς χ της ακτίνας

● d=d(x) η απόσταση των

σημείω ν Α(0, lnx) και
Β(χ, 0)

Έτσι
η απόσταση των σημείων

Α, Β είναι

d= (χ -χ ) +(y -y ) 2
2
2
1
2
1

= (χ-0 ) +(0-lnx ) 2
2

= χ +ln x
2
2

και σε συνάρτηση με τη μ ε -
ταβλητή χ

d(x) = χ +ln x
2
2

Eίναι
χ+ lnx
(χ +ln x )' 2χ+ 2 lnx×(lnx )' x
2
2
2
d'(x) =( χ +ln x)' = 2× χ +ln x = 2 × χ +ln x = χ +ln x
2

2
2
2
2
2
2
2
= χ +lnx
2
2
x× χ +ln x
Έτσι, οταν χ=e:
e +lne e +1
2
2
d'(e) = =
2
2
2
e× e +ln e e× e +1

2
( e +1 ) 2 e +1
2
= =
e× e +1 e
2
Επομένως,
ο ζητούμενος ρυθμός μ ε -
τaβολής είναι ίσος με
2
e +1
e

Τακης Τσακαλακος Κερκυρα 2017